0 attempts
0% avg
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | \[v_f^2 = v_i^2 + 2a\Delta x\] | Start with the kinematic relation connecting \(\Delta x\), \(v_i\), and \(v_f\). |
| 2 | \[0 = (22.5)^2 + 2(-9.8)\Delta x\] | At the highest point, \(v_x = 0\) and acceleration is downward (\(a = -9.8\,\text{m/s}^2\)). |
| 3 | \[\Delta x = \frac{(22.5)^2}{2\times 9.8}\] | Rearrange to solve for \(\Delta x\). |
| 4 | \[\boxed{\Delta x = 25.8\,\text{m}}\] | Compute the numerical value. |
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | \[v_f = v_i + at\] | Use the linear velocity–time equation. |
| 2 | \[0 = 22.5 + (-9.8)t\] | Set \(v_f = 0\) at the top. |
| 3 | \[t = \frac{22.5}{9.8}\] | Isolate \(t\). |
| 4 | \[\boxed{t = 2.30\,\text{s}}\] | Calculate the time to reach the highest point. |
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | \[t_{\text{total}} = 2t\] | Motion is symmetric; time up equals time down. |
| 2 | \[t_{\text{total}} = 2(2.30)\] | Substitute \(t\) from part (b). |
| 3 | \[\boxed{t_{\text{total}} = 4.59\,\text{s}}\] | Compute the total flight time. |
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | \[|v_f| = v_i\] | Returning to the same height, the magnitude of velocity equals the initial speed (since this projectile is symmetrical) . |
| 2 | \[\boxed{|v_f| = 22.5\,\text{m/s}}\] | Final answer. |
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | \[v_f = 0\] | Momentarily stops changing position at the peak. |
| 2 | \[a = -9.8\,\text{m/s}^2\] | Acceleration due to gravity is constant and downward. |
Just ask: "Help me solve this problem."
We'll help clarify entire units in one hour or less — guaranteed.
A horizontal spring with spring constant 162 N/m is compressed 50 cm and used to launch a 3 kg box across a frictionless, horizontal surface. After the box travels some distance, the surface becomes rough. The coefficient of kinetic friction of the box on the rough surface is 0.2. Find the total distance the box travels before stopping.
An object can move upward while having a downward acceleration.
A Corvette is traveling at a constant velocity \( 30 \, \text{m/s} \) when it passes a stationary supped up Civic. At that moment, the Civic puts the pedal to the floor and accelerates at \( 6 \, \text{m/s}^2 \). The Civic eventually catches up to the Corvette.
A spacecraft accelerates at a rate of \(20.0 \, \text{m/s}^2\).
A ball is dropped from the top of a tall building. At the same instant, a second ball is thrown upward from the ground level. When the two balls pass one another, one on the way up, the other on the way down, compare the magnitudes of their acceleration:
A student is running at her top speed of \( 5.0 \, \text{m/s} \) to catch a bus, which is stopped at the bus stop. When the student is still \( 40.0 \, \text{m} \) from the bus, it starts to pull away, moving with a constant acceleration of \( 0.170 \, \text{m/s}^2 \).
You are a bungee jumping fanatic and want to be the first bungee jumper on Jupiter. The length of your bungee cord is \( 45.0 \) \( \text{m} \). Free fall acceleration on Jupiter is \( 23.1 \) \( \text{m/s}^2 \). What is the ratio of your speed on Jupiter to your speed on Earth when you have dropped \( 45 \) \( \text{m} \)? Ignore the effects of air resistance and assume that you start at rest.
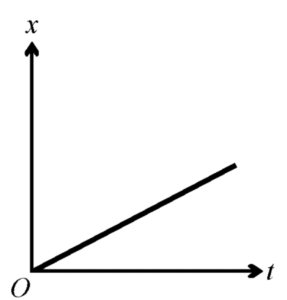 The displacement \(x\) of an object moving in one dimension is shown above as a function of time \(t\). The velocity of this object must be
The displacement \(x\) of an object moving in one dimension is shown above as a function of time \(t\). The velocity of this object must be
A baseball is seen to pass upward by a window with a vertical speed of \( 14 \) \( \text{m/s} \). If the ball was thrown by a person \( 18 \) \( \text{m} \) below on the street, determine the following.
A \( 1000 \) \( \text{kg} \) car is traveling east at \( 20 \) \( \text{m/s} \) when it collides perfectly inelastically with a northbound \( 2000 \) \( \text{kg} \) car traveling at \( 15 \) \( \text{m/s} \). If the coefficient of kinetic friction is \( 0.9 \), how far, and at what angle do the two cars skid before coming to a stop?
\(25.8\,\text{m}\)
\(2.30\,\text{s}\)
\(4.59\,\text{s}\)
\(22.5\,\text{m/s}\)
\(0\,\text{m/s};\,-9.8\,\text{m/s}^2\)
By continuing you (1) agree to our Terms of Use and Terms of Sale and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
| Kinematics | Forces |
|---|---|
| \(\Delta x = v_i t + \frac{1}{2} at^2\) | \(F = ma\) |
| \(v = v_i + at\) | \(F_g = \frac{G m_1 m_2}{r^2}\) |
| \(v^2 = v_i^2 + 2a \Delta x\) | \(f = \mu N\) |
| \(\Delta x = \frac{v_i + v}{2} t\) | \(F_s =-kx\) |
| \(v^2 = v_f^2 \,-\, 2a \Delta x\) |
| Circular Motion | Energy |
|---|---|
| \(F_c = \frac{mv^2}{r}\) | \(KE = \frac{1}{2} mv^2\) |
| \(a_c = \frac{v^2}{r}\) | \(PE = mgh\) |
| \(T = 2\pi \sqrt{\frac{r}{g}}\) | \(KE_i + PE_i = KE_f + PE_f\) |
| \(W = Fd \cos\theta\) |
| Momentum | Torque and Rotations |
|---|---|
| \(p = mv\) | \(\tau = r \cdot F \cdot \sin(\theta)\) |
| \(J = \Delta p\) | \(I = \sum mr^2\) |
| \(p_i = p_f\) | \(L = I \cdot \omega\) |
| Simple Harmonic Motion | Fluids |
|---|---|
| \(F = -kx\) | \(P = \frac{F}{A}\) |
| \(T = 2\pi \sqrt{\frac{l}{g}}\) | \(P_{\text{total}} = P_{\text{atm}} + \rho gh\) |
| \(T = 2\pi \sqrt{\frac{m}{k}}\) | \(Q = Av\) |
| \(x(t) = A \cos(\omega t + \phi)\) | \(F_b = \rho V g\) |
| \(a = -\omega^2 x\) | \(A_1v_1 = A_2v_2\) |
| Constant | Description |
|---|---|
| [katex]g[/katex] | Acceleration due to gravity, typically [katex]9.8 , \text{m/s}^2[/katex] on Earth’s surface |
| [katex]G[/katex] | Universal Gravitational Constant, [katex]6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2[/katex] |
| [katex]\mu_k[/katex] and [katex]\mu_s[/katex] | Coefficients of kinetic ([katex]\mu_k[/katex]) and static ([katex]\mu_s[/katex]) friction, dimensionless. Static friction ([katex]\mu_s[/katex]) is usually greater than kinetic friction ([katex]\mu_k[/katex]) as it resists the start of motion. |
| [katex]k[/katex] | Spring constant, in [katex]\text{N/m}[/katex] |
| [katex] M_E = 5.972 \times 10^{24} , \text{kg} [/katex] | Mass of the Earth |
| [katex] M_M = 7.348 \times 10^{22} , \text{kg} [/katex] | Mass of the Moon |
| [katex] M_M = 1.989 \times 10^{30} , \text{kg} [/katex] | Mass of the Sun |
| Variable | SI Unit |
|---|---|
| [katex]s[/katex] (Displacement) | [katex]\text{meters (m)}[/katex] |
| [katex]v[/katex] (Velocity) | [katex]\text{meters per second (m/s)}[/katex] |
| [katex]a[/katex] (Acceleration) | [katex]\text{meters per second squared (m/s}^2\text{)}[/katex] |
| [katex]t[/katex] (Time) | [katex]\text{seconds (s)}[/katex] |
| [katex]m[/katex] (Mass) | [katex]\text{kilograms (kg)}[/katex] |
| Variable | Derived SI Unit |
|---|---|
| [katex]F[/katex] (Force) | [katex]\text{newtons (N)}[/katex] |
| [katex]E[/katex], [katex]PE[/katex], [katex]KE[/katex] (Energy, Potential Energy, Kinetic Energy) | [katex]\text{joules (J)}[/katex] |
| [katex]P[/katex] (Power) | [katex]\text{watts (W)}[/katex] |
| [katex]p[/katex] (Momentum) | [katex]\text{kilogram meters per second (kgm/s)}[/katex] |
| [katex]\omega[/katex] (Angular Velocity) | [katex]\text{radians per second (rad/s)}[/katex] |
| [katex]\tau[/katex] (Torque) | [katex]\text{newton meters (Nm)}[/katex] |
| [katex]I[/katex] (Moment of Inertia) | [katex]\text{kilogram meter squared (kgm}^2\text{)}[/katex] |
| [katex]f[/katex] (Frequency) | [katex]\text{hertz (Hz)}[/katex] |
Metric Prefixes
Example of using unit analysis: Convert 5 kilometers to millimeters.
Start with the given measurement: [katex]\text{5 km}[/katex]
Use the conversion factors for kilometers to meters and meters to millimeters: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}}[/katex]
Perform the multiplication: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}} = 5 \times 10^3 \times 10^3 \, \text{mm}[/katex]
Simplify to get the final answer: [katex]\boxed{5 \times 10^6 \, \text{mm}}[/katex]
Prefix | Symbol | Power of Ten | Equivalent |
|---|---|---|---|
Pico- | p | [katex]10^{-12}[/katex] | 0.000000000001 |
Nano- | n | [katex]10^{-9}[/katex] | 0.000000001 |
Micro- | µ | [katex]10^{-6}[/katex] | 0.000001 |
Milli- | m | [katex]10^{-3}[/katex] | 0.001 |
Centi- | c | [katex]10^{-2}[/katex] | 0.01 |
Deci- | d | [katex]10^{-1}[/katex] | 0.1 |
(Base unit) | – | [katex]10^{0}[/katex] | 1 |
Deca- or Deka- | da | [katex]10^{1}[/katex] | 10 |
Hecto- | h | [katex]10^{2}[/katex] | 100 |
Kilo- | k | [katex]10^{3}[/katex] | 1,000 |
Mega- | M | [katex]10^{6}[/katex] | 1,000,000 |
Giga- | G | [katex]10^{9}[/katex] | 1,000,000,000 |
Tera- | T | [katex]10^{12}[/katex] | 1,000,000,000,000 |
One price to unlock most advanced version of Phy across all our tools.
per month
Billed Monthly. Cancel Anytime.
We crafted THE Ultimate A.P Physics 1 Program so you can learn faster and score higher.
Try our free calculator to see what you need to get a 5 on the 2026 AP Physics 1 exam.
A quick explanation
Credits are used to grade your FRQs and GQs. Pro users get unlimited credits.
Submitting counts as 1 attempt.
Viewing answers or explanations count as a failed attempts.
Phy gives partial credit if needed
MCQs and GQs are are 1 point each. FRQs will state points for each part.
Phy customizes problem explanations based on what you struggle with. Just hit the explanation button to see.
Understand you mistakes quicker.
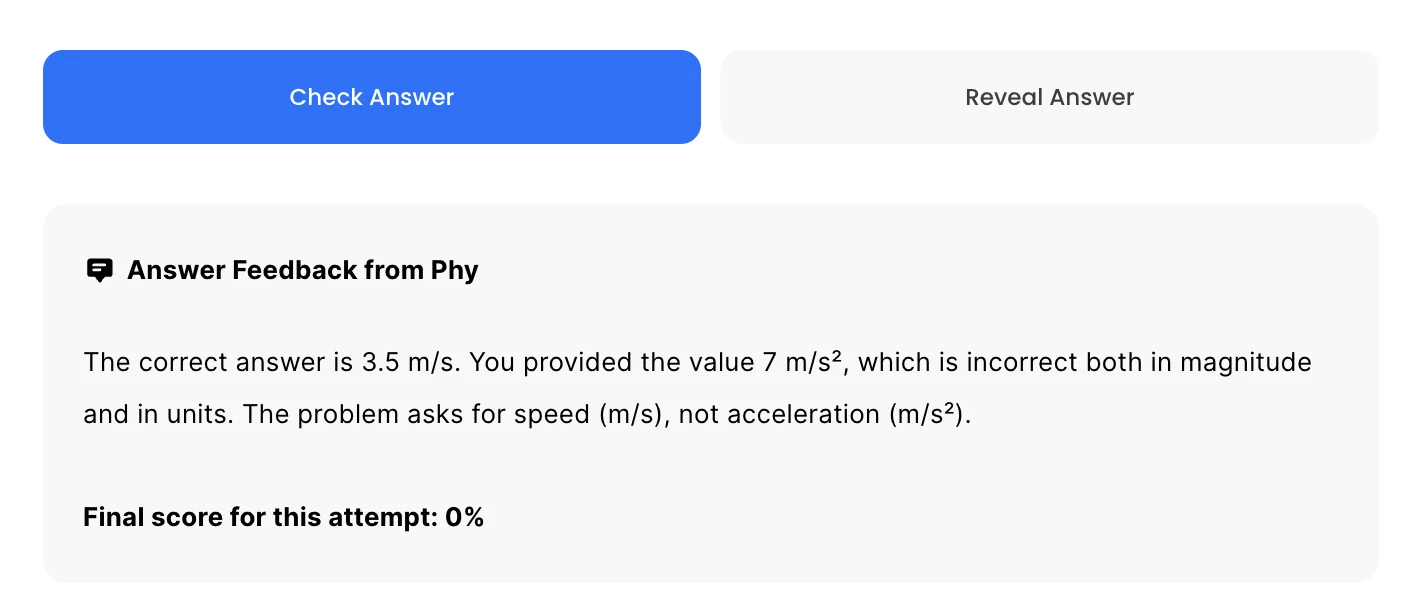
Phy automatically provides feedback so you can improve your responses.
10 Free Credits To Get You Started
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.
Feeling uneasy about your next physics test? We'll boost your grade in 3 lessons or less—guaranteed
NEW! PHY AI accurately solves all questions
🔥 Get up to 30% off Elite Physics Tutoring
🧠 NEW! Learn Physics From Scratch Self Paced Course
🎯 Need exam style practice questions?