| Derivation or Formula | Reasoning |
|---|---|
| \[W_{\text{air}} = \rho_{\text{rock}} V g\] | This is the full weight of the rock in air, where \(\rho_{\text{rock}}\) is the rock density, \(V\) is its volume, and \(g\) is gravitational acceleration. |
| \[W_{\text{water}} = \rho_{\text{rock}}Vg – \rho_{\text{water}}Vg\] | The apparent weight when submerged is the true weight minus the buoyant force, which equals the weight of the displaced water \((\rho_{\text{water}}Vg)\). |
| \[\rho_{\text{rock}}Vg – \rho_{\text{water}}Vg = \tfrac{1}{2}\,\rho_{\text{rock}}Vg\] | The problem states the rock weighs twice as much in air as in water, so \(W_{\text{water}} = \tfrac{1}{2}W_{\text{air}}\). Substitute \(W_{\text{air}}\) above. |
| \[\rho_{\text{rock}} – \rho_{\text{water}} = \tfrac{1}{2}\,\rho_{\text{rock}}\] | Canceling the common factors \(Vg\) from both sides simplifies the equation. |
| \[2\,\rho_{\text{rock}} – 2\,\rho_{\text{water}} = \rho_{\text{rock}}\] | Multiply both sides by 2 to clear the fraction. |
| \[\rho_{\text{rock}} = 2\,\rho_{\text{water}}\] | Solve for \(\rho_{\text{rock}}\) by subtracting \(\rho_{\text{rock}}\) from both sides. |
| \[\rho_{\text{rock}} = 2 \times 1000\,\text{kg/m}^3 = \boxed{2000\,\text{kg/m}^3}\] | Assuming the density of water is \(1000\,\text{kg/m}^3\), the rock density becomes \(2000\,\text{kg/m}^3\) (to 3 significant figures). |
| Derivation or Formula | Reasoning |
|---|---|
| \[\rho_{\text{avg}} = p\,\rho_{\text{quartz}} + (1-p)\times0 = p\,\rho_{\text{quartz}}\] | The rock is part solid quartz and part hollow (air). Since the density of air is negligible, \(\rho_{\text{avg}}\) is just the fraction \(p\) of quartz times the density of quartz \(\rho_{\text{quartz}}\). |
| \[p = \tfrac{\rho_{\text{avg}}}{\rho_{\text{quartz}}}\] | Solve for \(p\) (the fraction that is solid quartz) using the average density, which we determined as \(2000\,\text{kg/m}^3\), and the given quartz density \(2660\,\text{kg/m}^3\). |
| \[p = \tfrac{2000}{2660} \approx 0.752\] | Calculate \(p\) to determine the fraction of the rock that is quartz. |
| \[\text{Percentage hollow} = (1-p) \times 100\% \approx (1-0.752) \times 100\% \approx \boxed{24.8\%}\] | The remainder of the rock (\(1-p\)) is hollow. Converting to a percentage gives about 24.8\% hollow, to 3 significant figures. |
A Major Upgrade To Phy Is Coming Soon — Stay Tuned
We'll help clarify entire units in one hour or less — guaranteed.
A self paced course with videos, problems sets, and everything you need to get a 5. Trusted by over 15k students and over 200 schools.
An object is suspended from a spring scale first in air, then in water, as shown in the figure above. The spring scale reading in air is \( 17.8 \) \( \text{N} \), and the spring scale reading when the object is completely submerged in water is \( 16.2 \) \( \text{N} \). The density of water is \( 1000 \) \( \text{kg/m}^3 \).
How large must a heating duct be if air moving \( 3 \ \frac{\text{m}}{\text{s}} \) along it can replenish the air in a room of \( 300 \ \text{m}^3 \) volume every \( 15 \) minutes? Assume the air’s density remains constant.
Why do you float higher in salt water than in fresh water?
Water flows from point \( A \) to points \( D \) and \( E \) as shown. Some of the flow parameters are known, as shown in the table. Determine the unknown parameters. Note the diagram above does not show the relative diameters of each section of the pipe.
| Section | Diameter | Flow Rate | Velocity |
|---|---|---|---|
| \( \text{AB} \) | \( 300 \) \( \text{mm} \) | \(\textbf{?}\) | \(\textbf{?}\) |
| \( \text{BC} \) | \( 600 \) \( \text{mm} \) | \(\textbf{?}\) | \( 1.2 \) \( \text{m/s} \) |
| \( \text{CD} \) | \(\textbf{?}\) | \( Q_{CD} = 2Q_{CE} \) \( \text{m}^3/\text{s} \) | \( 1.4 \) \( \text{m/s} \) |
| \( \text{CE} \) | \( 150 \) \( \text{mm} \) | \( Q_{CE} = 0.5Q_{CD} \) \( \text{m}^3/\text{s} \) | \(\textbf{?}\) |
Two paper cups are suspended by strings and hung near each other. They are separated by about \( 10 \) \( \text{cm} \). Explain what happens to the cups when you blow air between them. Hint: Do they remain still, moves away from each other or move towards each other?
Wanda watches the fish in her fish tank and notices that the angelfish like to feed at the water’s surface, while the catfish feed \( 0.300 \) \( \text{m} \) below at the bottom of the tank. If the average density of the water in the tank is \( 1000\) \( \text{kg/m}^3 \), what is the absolute pressure on the catfish?
Which of the following statements is an expression of the equation of continuity?
In a carbonated drink dispenser, bubbles flow through a horizontal tube that gradually narrows in diameter. Assuming the change in height is negligible, which of the following best describes how the bubbles behave as they move from the wider section of the tube to the narrower section?
Two objects labeled K and L have equal mass but densities \( 0.95D_o \) and \( D_o \), respectively. Each of these objects floats after being thrown into a deep swimming pool. Which is true about the buoyant forces acting on these objects?
A sample of an unknown material appears to weigh \( 285 \) \( \text{N} \) in air and \( 195 \) \( \text{N} \) when immersed in alcohol of specific gravity \( 0.700 \).
By continuing you (1) agree to our Terms of Use and Terms of Sale and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
| Kinematics | Forces |
|---|---|
| \(\Delta x = v_i t + \frac{1}{2} at^2\) | \(F = ma\) |
| \(v = v_i + at\) | \(F_g = \frac{G m_1 m_2}{r^2}\) |
| \(v^2 = v_i^2 + 2a \Delta x\) | \(f = \mu N\) |
| \(\Delta x = \frac{v_i + v}{2} t\) | \(F_s =-kx\) |
| \(v^2 = v_f^2 \,-\, 2a \Delta x\) |
| Circular Motion | Energy |
|---|---|
| \(F_c = \frac{mv^2}{r}\) | \(KE = \frac{1}{2} mv^2\) |
| \(a_c = \frac{v^2}{r}\) | \(PE = mgh\) |
| \(T = 2\pi \sqrt{\frac{r}{g}}\) | \(KE_i + PE_i = KE_f + PE_f\) |
| \(W = Fd \cos\theta\) |
| Momentum | Torque and Rotations |
|---|---|
| \(p = mv\) | \(\tau = r \cdot F \cdot \sin(\theta)\) |
| \(J = \Delta p\) | \(I = \sum mr^2\) |
| \(p_i = p_f\) | \(L = I \cdot \omega\) |
| Simple Harmonic Motion | Fluids |
|---|---|
| \(F = -kx\) | \(P = \frac{F}{A}\) |
| \(T = 2\pi \sqrt{\frac{l}{g}}\) | \(P_{\text{total}} = P_{\text{atm}} + \rho gh\) |
| \(T = 2\pi \sqrt{\frac{m}{k}}\) | \(Q = Av\) |
| \(x(t) = A \cos(\omega t + \phi)\) | \(F_b = \rho V g\) |
| \(a = -\omega^2 x\) | \(A_1v_1 = A_2v_2\) |
| Constant | Description |
|---|---|
| [katex]g[/katex] | Acceleration due to gravity, typically [katex]9.8 , \text{m/s}^2[/katex] on Earth’s surface |
| [katex]G[/katex] | Universal Gravitational Constant, [katex]6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2[/katex] |
| [katex]\mu_k[/katex] and [katex]\mu_s[/katex] | Coefficients of kinetic ([katex]\mu_k[/katex]) and static ([katex]\mu_s[/katex]) friction, dimensionless. Static friction ([katex]\mu_s[/katex]) is usually greater than kinetic friction ([katex]\mu_k[/katex]) as it resists the start of motion. |
| [katex]k[/katex] | Spring constant, in [katex]\text{N/m}[/katex] |
| [katex] M_E = 5.972 \times 10^{24} , \text{kg} [/katex] | Mass of the Earth |
| [katex] M_M = 7.348 \times 10^{22} , \text{kg} [/katex] | Mass of the Moon |
| [katex] M_M = 1.989 \times 10^{30} , \text{kg} [/katex] | Mass of the Sun |
| Variable | SI Unit |
|---|---|
| [katex]s[/katex] (Displacement) | [katex]\text{meters (m)}[/katex] |
| [katex]v[/katex] (Velocity) | [katex]\text{meters per second (m/s)}[/katex] |
| [katex]a[/katex] (Acceleration) | [katex]\text{meters per second squared (m/s}^2\text{)}[/katex] |
| [katex]t[/katex] (Time) | [katex]\text{seconds (s)}[/katex] |
| [katex]m[/katex] (Mass) | [katex]\text{kilograms (kg)}[/katex] |
| Variable | Derived SI Unit |
|---|---|
| [katex]F[/katex] (Force) | [katex]\text{newtons (N)}[/katex] |
| [katex]E[/katex], [katex]PE[/katex], [katex]KE[/katex] (Energy, Potential Energy, Kinetic Energy) | [katex]\text{joules (J)}[/katex] |
| [katex]P[/katex] (Power) | [katex]\text{watts (W)}[/katex] |
| [katex]p[/katex] (Momentum) | [katex]\text{kilogram meters per second (kgm/s)}[/katex] |
| [katex]\omega[/katex] (Angular Velocity) | [katex]\text{radians per second (rad/s)}[/katex] |
| [katex]\tau[/katex] (Torque) | [katex]\text{newton meters (Nm)}[/katex] |
| [katex]I[/katex] (Moment of Inertia) | [katex]\text{kilogram meter squared (kgm}^2\text{)}[/katex] |
| [katex]f[/katex] (Frequency) | [katex]\text{hertz (Hz)}[/katex] |
Metric Prefixes
Example of using unit analysis: Convert 5 kilometers to millimeters.
Start with the given measurement: [katex]\text{5 km}[/katex]
Use the conversion factors for kilometers to meters and meters to millimeters: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}}[/katex]
Perform the multiplication: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}} = 5 \times 10^3 \times 10^3 \, \text{mm}[/katex]
Simplify to get the final answer: [katex]\boxed{5 \times 10^6 \, \text{mm}}[/katex]
Prefix | Symbol | Power of Ten | Equivalent |
|---|---|---|---|
Pico- | p | [katex]10^{-12}[/katex] | |
Nano- | n | [katex]10^{-9}[/katex] | |
Micro- | µ | [katex]10^{-6}[/katex] | |
Milli- | m | [katex]10^{-3}[/katex] | |
Centi- | c | [katex]10^{-2}[/katex] | |
Deci- | d | [katex]10^{-1}[/katex] | |
(Base unit) | – | [katex]10^{0}[/katex] | |
Deca- or Deka- | da | [katex]10^{1}[/katex] | |
Hecto- | h | [katex]10^{2}[/katex] | |
Kilo- | k | [katex]10^{3}[/katex] | |
Mega- | M | [katex]10^{6}[/katex] | |
Giga- | G | [katex]10^{9}[/katex] | |
Tera- | T | [katex]10^{12}[/katex] |
One price to unlock most advanced version of Phy across all our tools.
per month
Billed Monthly. Cancel Anytime.
We crafted THE Ultimate A.P Physics 1 Program so you can learn faster and score higher.
Try our free calculator to see what you need to get a 5 on the 2026 AP Physics 1 exam.
Understand you mistakes quicker.
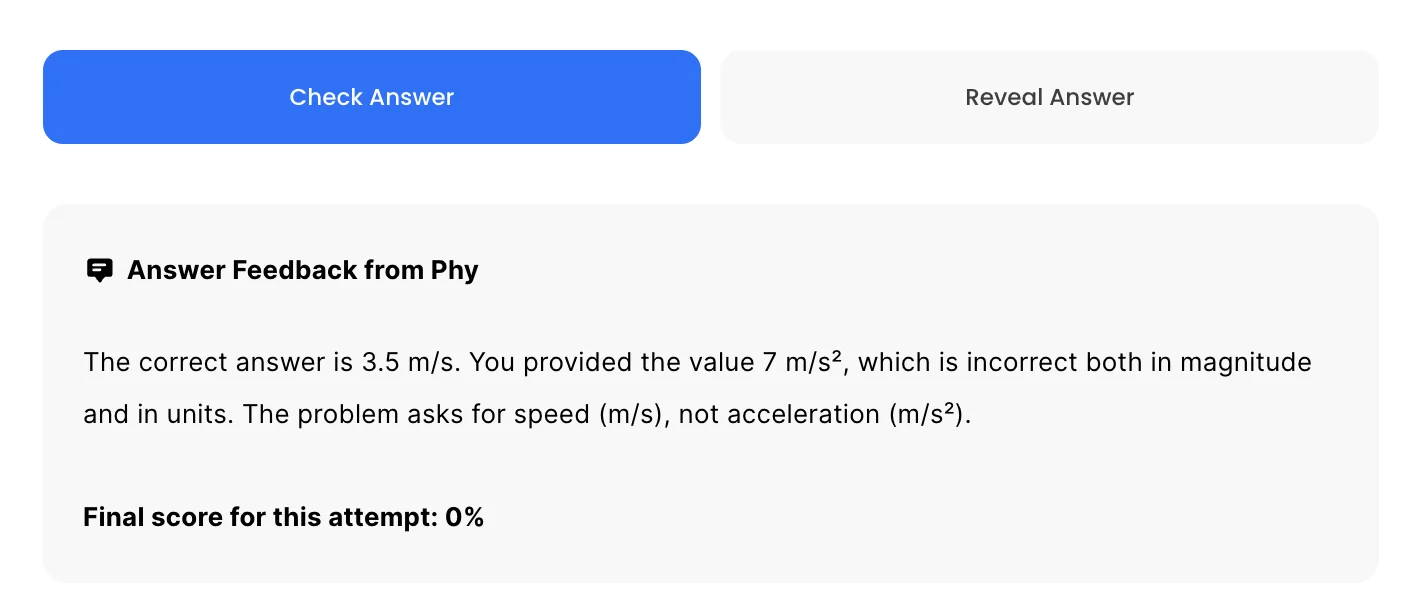
Phy automatically provides feedback so you can improve your responses.
10 Free Credits To Get You Started
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.
Feeling uneasy about your next physics test? We'll boost your grade in 3 lessons or less—guaranteed
