0 attempts
0% avg
| Derivation/Formula | Reasoning |
|---|---|
| $$\frac{1}{2} m v_i^2 = \frac{1}{2} m v_x^2 + m g \Delta x$$ | Mechanical energy is conserved; initial kinetic changes into kinetic plus gravitational potential after rising by \(\Delta x = 13\text{ m}\). |
| $$v_x^2 = v_i^2 – 2 g \Delta x$$ | Algebraically solve the previous equation for \(v_x\). |
| $$v_x = \sqrt{v_i^2 – 2 g \Delta x}$$ | Take the square root to obtain speed magnitude. |
| $$v_x = \sqrt{(24.0)^2 – 2 (9.8)(13.0)}\;\text{m/s}$$ | Insert \(v_i = 24.0\text{ m/s}\), \(g = 9.8\text{ m/s}^2\), and \(\Delta x = 13.0\text{ m}\). |
| $$\boxed{v_x \approx 17.9\ \text{m/s}}$$ | Numeric result; direction can be up or down, magnitude shown. |
| Derivation/Formula | Reasoning |
|---|---|
| $$\Delta x = v_i t + \frac{1}{2} a t^2$$ | Kinematic displacement equation with upward positive. |
| $$13 = 24 t – 4.9 t^2$$ | Substitute \(\Delta x = 13\), \(v_i = 24\text{ m/s}\), \(a = -g = -9.8\text{ m/s}^2\). |
| $$4.9 t^2 – 24 t + 13 = 0$$ | Rearrange into standard quadratic form. |
| $$t = \frac{24 \pm \sqrt{24^2 – 4(4.9)(13)}}{2(4.9)}$$ | Apply the quadratic formula to solve for \(t\). |
| $$t = \frac{24 \pm 17.9}{9.8}$$ | Evaluate the discriminant \(\sqrt{321.2} \approx 17.9\). |
| $$t_1 \approx 0.62\ \text{s},\qquad t_2 \approx 4.28\ \text{s}$$ | Compute the two positive roots. |
| $$\boxed{t = 0.62\ \text{s}\ \text{or}\ 4.28\ \text{s}}$$ | Both times are physically valid. |
| Derivation/Formula | Reasoning |
|---|---|
| $$t_1 \text{ (ascending)},\; t_2 \text{ (descending)}$$ | The quadratic gives two roots because the stone passes the \(13\text{ m}\) level once while going up and again while coming down after reaching its peak. |
Just ask: "Help me solve this problem."
We'll help clarify entire units in one hour or less — guaranteed.
Mary and Sally are in a foot race. When Mary is \( 22 \) \( \text{m} \) from the finish line, she has a speed of \( 4.0 \) \( \text{m/s} \) and is \( 5.0 \) \( \text{m} \) behind Sally, who has a speed of \( 5.0 \) \( \text{m/s} \). Sally thinks she has an easy win and, during the remaining portion of the race, decelerates at a constant rate of \( 0.40 \) \( \text{m/s}^2 \) until she reaches the finish line. What constant acceleration must Mary maintain during the remaining portion of the race if she wishes to cross the finish line side-by-side with Sally?
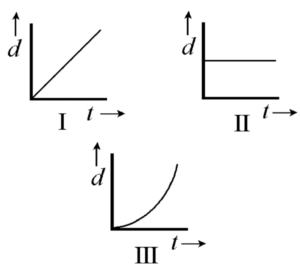
In which of the following is the rate of change of the particle’s momentum zero?
A ball is dropped from a window [katex]10 \, [/katex] above the sidewalk. Determine the time it takes for the ball to fall to the sidewalk.
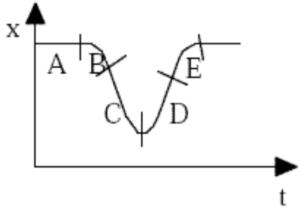 The graph below is a plot of position versus time. For which labeled segments is the velocity positive and the acceleration negative?
The graph below is a plot of position versus time. For which labeled segments is the velocity positive and the acceleration negative?

Which statement is true about the distances the two objects have traveled at time \( t_f \)?
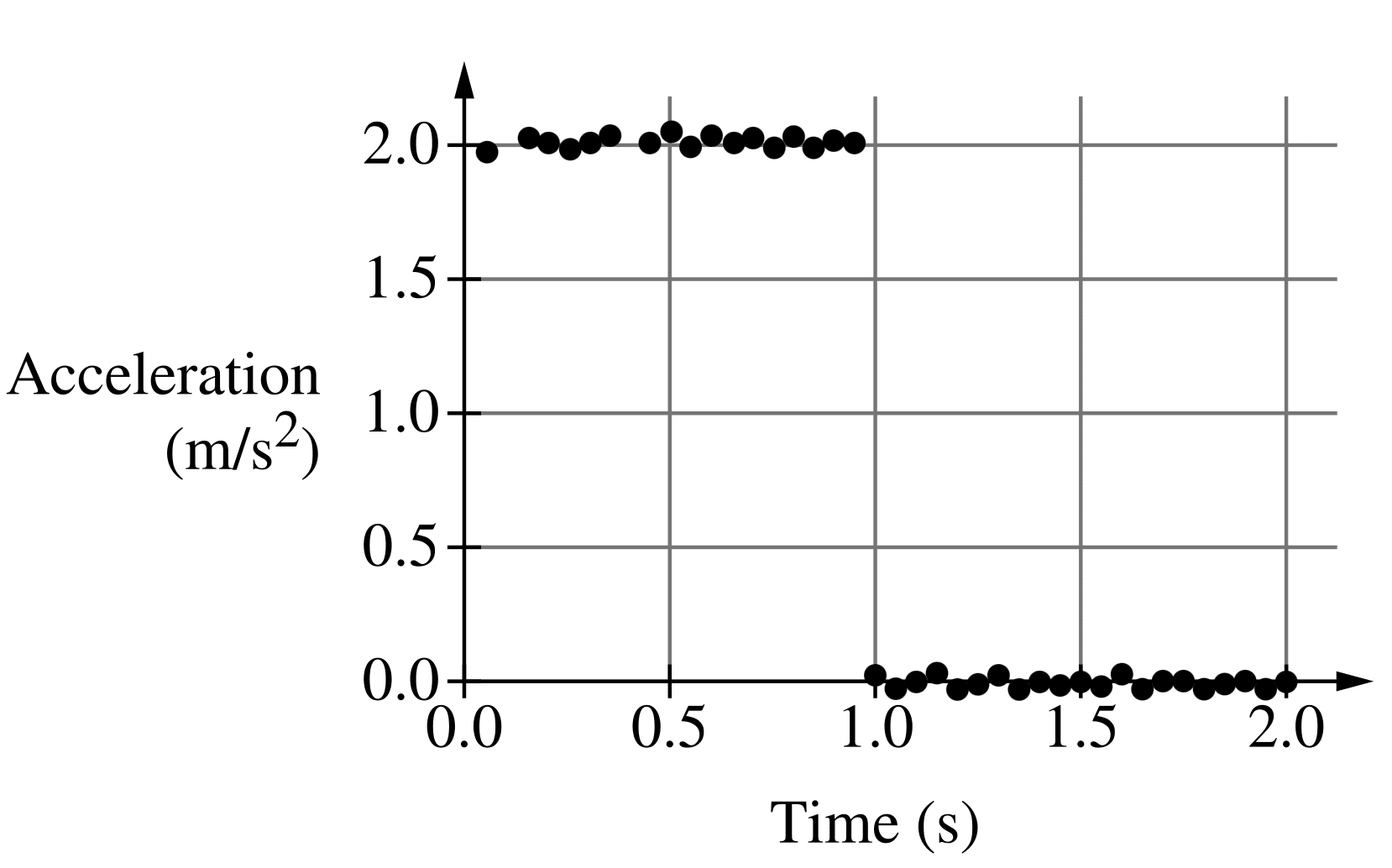
The graph shows the acceleration as a function of time for an object that is at rest at time \( t = 0 \) \( \text{s} \). The distance traveled by the object between \( 0 \) and \( 2 \) \( \text{s} \) is most nearly
An elevator starts at rest on the ground floor. It accelerates upward smoothly for \( 2 \) \( \text{s} \) until reaching a steady upward speed. It continues at that constant speed for \( 5 \) \( \text{s} \) before gently slowing to rest at the next floor in \( 3 \) \( \text{s} \). Draw the velocity vs. time graph.
A blue ball is thrown upward with a velocity of \( 9 \) \( \text{m/s} \) upward from the top of a high cliff. At the same time, a red ball is dropped from the same spot. The red ball is observed to hit the ground below exactly \( 1 \) \( \text{s} \) before the blue ball. How high is the cliff?
a: \(17.9\ \text{m/s}\)
b: \(0.62\ \text{s}\) or \(4.28\ \text{s}\)
c: \(\text{Upward and downward pass}\)
By continuing you (1) agree to our Terms of Use and Terms of Sale and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
| Kinematics | Forces |
|---|---|
| \(\Delta x = v_i t + \frac{1}{2} at^2\) | \(F = ma\) |
| \(v = v_i + at\) | \(F_g = \frac{G m_1 m_2}{r^2}\) |
| \(v^2 = v_i^2 + 2a \Delta x\) | \(f = \mu N\) |
| \(\Delta x = \frac{v_i + v}{2} t\) | \(F_s =-kx\) |
| \(v^2 = v_f^2 \,-\, 2a \Delta x\) |
| Circular Motion | Energy |
|---|---|
| \(F_c = \frac{mv^2}{r}\) | \(KE = \frac{1}{2} mv^2\) |
| \(a_c = \frac{v^2}{r}\) | \(PE = mgh\) |
| \(T = 2\pi \sqrt{\frac{r}{g}}\) | \(KE_i + PE_i = KE_f + PE_f\) |
| \(W = Fd \cos\theta\) |
| Momentum | Torque and Rotations |
|---|---|
| \(p = mv\) | \(\tau = r \cdot F \cdot \sin(\theta)\) |
| \(J = \Delta p\) | \(I = \sum mr^2\) |
| \(p_i = p_f\) | \(L = I \cdot \omega\) |
| Simple Harmonic Motion | Fluids |
|---|---|
| \(F = -kx\) | \(P = \frac{F}{A}\) |
| \(T = 2\pi \sqrt{\frac{l}{g}}\) | \(P_{\text{total}} = P_{\text{atm}} + \rho gh\) |
| \(T = 2\pi \sqrt{\frac{m}{k}}\) | \(Q = Av\) |
| \(x(t) = A \cos(\omega t + \phi)\) | \(F_b = \rho V g\) |
| \(a = -\omega^2 x\) | \(A_1v_1 = A_2v_2\) |
| Constant | Description |
|---|---|
| [katex]g[/katex] | Acceleration due to gravity, typically [katex]9.8 , \text{m/s}^2[/katex] on Earth’s surface |
| [katex]G[/katex] | Universal Gravitational Constant, [katex]6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2[/katex] |
| [katex]\mu_k[/katex] and [katex]\mu_s[/katex] | Coefficients of kinetic ([katex]\mu_k[/katex]) and static ([katex]\mu_s[/katex]) friction, dimensionless. Static friction ([katex]\mu_s[/katex]) is usually greater than kinetic friction ([katex]\mu_k[/katex]) as it resists the start of motion. |
| [katex]k[/katex] | Spring constant, in [katex]\text{N/m}[/katex] |
| [katex] M_E = 5.972 \times 10^{24} , \text{kg} [/katex] | Mass of the Earth |
| [katex] M_M = 7.348 \times 10^{22} , \text{kg} [/katex] | Mass of the Moon |
| [katex] M_M = 1.989 \times 10^{30} , \text{kg} [/katex] | Mass of the Sun |
| Variable | SI Unit |
|---|---|
| [katex]s[/katex] (Displacement) | [katex]\text{meters (m)}[/katex] |
| [katex]v[/katex] (Velocity) | [katex]\text{meters per second (m/s)}[/katex] |
| [katex]a[/katex] (Acceleration) | [katex]\text{meters per second squared (m/s}^2\text{)}[/katex] |
| [katex]t[/katex] (Time) | [katex]\text{seconds (s)}[/katex] |
| [katex]m[/katex] (Mass) | [katex]\text{kilograms (kg)}[/katex] |
| Variable | Derived SI Unit |
|---|---|
| [katex]F[/katex] (Force) | [katex]\text{newtons (N)}[/katex] |
| [katex]E[/katex], [katex]PE[/katex], [katex]KE[/katex] (Energy, Potential Energy, Kinetic Energy) | [katex]\text{joules (J)}[/katex] |
| [katex]P[/katex] (Power) | [katex]\text{watts (W)}[/katex] |
| [katex]p[/katex] (Momentum) | [katex]\text{kilogram meters per second (kgm/s)}[/katex] |
| [katex]\omega[/katex] (Angular Velocity) | [katex]\text{radians per second (rad/s)}[/katex] |
| [katex]\tau[/katex] (Torque) | [katex]\text{newton meters (Nm)}[/katex] |
| [katex]I[/katex] (Moment of Inertia) | [katex]\text{kilogram meter squared (kgm}^2\text{)}[/katex] |
| [katex]f[/katex] (Frequency) | [katex]\text{hertz (Hz)}[/katex] |
Metric Prefixes
Example of using unit analysis: Convert 5 kilometers to millimeters.
Start with the given measurement: [katex]\text{5 km}[/katex]
Use the conversion factors for kilometers to meters and meters to millimeters: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}}[/katex]
Perform the multiplication: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}} = 5 \times 10^3 \times 10^3 \, \text{mm}[/katex]
Simplify to get the final answer: [katex]\boxed{5 \times 10^6 \, \text{mm}}[/katex]
Prefix | Symbol | Power of Ten | Equivalent |
|---|---|---|---|
Pico- | p | [katex]10^{-12}[/katex] | 0.000000000001 |
Nano- | n | [katex]10^{-9}[/katex] | 0.000000001 |
Micro- | µ | [katex]10^{-6}[/katex] | 0.000001 |
Milli- | m | [katex]10^{-3}[/katex] | 0.001 |
Centi- | c | [katex]10^{-2}[/katex] | 0.01 |
Deci- | d | [katex]10^{-1}[/katex] | 0.1 |
(Base unit) | – | [katex]10^{0}[/katex] | 1 |
Deca- or Deka- | da | [katex]10^{1}[/katex] | 10 |
Hecto- | h | [katex]10^{2}[/katex] | 100 |
Kilo- | k | [katex]10^{3}[/katex] | 1,000 |
Mega- | M | [katex]10^{6}[/katex] | 1,000,000 |
Giga- | G | [katex]10^{9}[/katex] | 1,000,000,000 |
Tera- | T | [katex]10^{12}[/katex] | 1,000,000,000,000 |
One price to unlock most advanced version of Phy across all our tools.
per month
Billed Monthly. Cancel Anytime.
We crafted THE Ultimate A.P Physics 1 Program so you can learn faster and score higher.
Try our free calculator to see what you need to get a 5 on the 2026 AP Physics 1 exam.
A quick explanation
Credits are used to grade your FRQs and GQs. Pro users get unlimited credits.
Submitting counts as 1 attempt.
Viewing answers or explanations count as a failed attempts.
Phy gives partial credit if needed
MCQs and GQs are are 1 point each. FRQs will state points for each part.
Phy customizes problem explanations based on what you struggle with. Just hit the explanation button to see.
Understand you mistakes quicker.
Phy automatically provides feedback so you can improve your responses.
10 Free Credits To Get You Started
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.
Feeling uneasy about your next physics test? We'll boost your grade in 3 lessons or less—guaranteed
NEW! PHY AI accurately solves all questions
🔥 Get up to 30% off Elite Physics Tutoring
🧠 NEW! Learn Physics From Scratch Self Paced Course
🎯 Need exam style practice questions?