0 attempts
0% avg
UBQ Credits
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | Determine initial speed (\( v_0 \)) using projectile motion:
Horizontal motion: Vertical motion: Since \( t = \dfrac{\Delta x}{v_0 \cos \theta} \), substitute into vertical equation: |
Set up equations for horizontal and vertical motion to solve for initial speed \( v_0 \). Note that both displacement and acceleration due to gravity point down. |
| 2 | Simplify and solve for \( v_0 \):
\( -2.0 = 54 \tan 30^\circ – \dfrac{1}{2} \times 9.8 \times \dfrac{54^2}{v_0^2 \cos^2 30^\circ} \) Calculate constants: Substitute values and solve for \( v_0 \): |
Simplified the equation to make \( v_0 \) the subject and substituted known values. |
| 3 | Calculate \( v_0 \):
\( -2.0 = 54 \times 0.5774 – \dfrac{4.9 \times 54^2}{v_0^2 \times 0.75} \) |
Solved for the initial speed \( v_0 \). |
| 4 | (a) Use the final speed to find acceleration during the throw:
Use \( v_f^2 = v_i^2 + 2 a s \) |
Calculated acceleration using kinematic equation. |
| 5 | (b) Find time of flight:
\( t = \dfrac{\Delta x}{v_0 \cos \theta} \) |
Used horizontal motion to calculate total time. |
Just ask: "Help me solve this problem."
We'll help clarify entire units in one hour or less — guaranteed.
Measurements made in 1910 indicate that the common flea is an impressive jumper, given its size. Assume that a flea’s initial speed is 2.1 m/s, and that it leaps at an angle of 21° with respect to the horizontal. The jump lasts 0.16 s.
A bald eagle in level flight at a height of \(135 \, \text{m}\) drops the fish it caught. If the eagle’s speed is \(25.0 \, \text{m/s}\) how far from the drop point will the fish land?
The highest barrier that a projectile can clear is 16.2 m, when the projectile is launched at an angle of 22.0° above the horizontal. What is the projectile’s launch speed?
Wile E. Coyote is (still) chasing after his arch-nemesis, the Roadrunner across a cliff that is \(125 \, \text{m}\) high. The Coyote is running in the horizontal direction towards the edge of a cliff when, at the last second, the Roadrunner steps out of the way and the witless coyote falls to the canyon floor.
Which launch angle gives the greatest horizontal range, assuming level ground and no air resistance?
Water balloons are tossed from the roof of a building, all with the same speed but with different launch angles. Which one has the highest speed when it hits the ground? Ignore air resistance. Without using equations, explain your answer.
A rocket is fired at a speed of 75.0 m/s from ground level, at an angle of 60.0° above the horizontal. The rocket is fired toward an 11.0-m-high wall, which is located 27.0 m away. The rocket attains its launch speed in a negligibly short period of time, after which its engines shut down and the rocket coasts. By how much does the rocket clear the top of the wall?
If a baseball pitch leaves the pitcher’s hand horizontally at a velocity of \( 150 \) \( \text{km/h} \), by what \( \% \) will the pull of gravity change the magnitude of the velocity when the ball reaches the batter, \( 18 \) \( \text{m} \) away? For this estimate, ignore air resistance and spin on the ball.
A officer fires a pistol horizontally toward a target \(120 \,\text{m}\) at a velocity of \(200 \, \text{m/s}\). If the officer aimed directly at the bull’s eye
Which statements are not valid for a projectile? Take up as positive.
By continuing you (1) agree to our Terms of Use and Terms of Sale and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
| Kinematics | Forces |
|---|---|
| \(\Delta x = v_i t + \frac{1}{2} at^2\) | \(F = ma\) |
| \(v = v_i + at\) | \(F_g = \frac{G m_1 m_2}{r^2}\) |
| \(v^2 = v_i^2 + 2a \Delta x\) | \(f = \mu N\) |
| \(\Delta x = \frac{v_i + v}{2} t\) | \(F_s =-kx\) |
| \(v^2 = v_f^2 \,-\, 2a \Delta x\) |
| Circular Motion | Energy |
|---|---|
| \(F_c = \frac{mv^2}{r}\) | \(KE = \frac{1}{2} mv^2\) |
| \(a_c = \frac{v^2}{r}\) | \(PE = mgh\) |
| \(T = 2\pi \sqrt{\frac{r}{g}}\) | \(KE_i + PE_i = KE_f + PE_f\) |
| \(W = Fd \cos\theta\) |
| Momentum | Torque and Rotations |
|---|---|
| \(p = mv\) | \(\tau = r \cdot F \cdot \sin(\theta)\) |
| \(J = \Delta p\) | \(I = \sum mr^2\) |
| \(p_i = p_f\) | \(L = I \cdot \omega\) |
| Simple Harmonic Motion | Fluids |
|---|---|
| \(F = -kx\) | \(P = \frac{F}{A}\) |
| \(T = 2\pi \sqrt{\frac{l}{g}}\) | \(P_{\text{total}} = P_{\text{atm}} + \rho gh\) |
| \(T = 2\pi \sqrt{\frac{m}{k}}\) | \(Q = Av\) |
| \(x(t) = A \cos(\omega t + \phi)\) | \(F_b = \rho V g\) |
| \(a = -\omega^2 x\) | \(A_1v_1 = A_2v_2\) |
| Constant | Description |
|---|---|
| [katex]g[/katex] | Acceleration due to gravity, typically [katex]9.8 , \text{m/s}^2[/katex] on Earth’s surface |
| [katex]G[/katex] | Universal Gravitational Constant, [katex]6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2[/katex] |
| [katex]\mu_k[/katex] and [katex]\mu_s[/katex] | Coefficients of kinetic ([katex]\mu_k[/katex]) and static ([katex]\mu_s[/katex]) friction, dimensionless. Static friction ([katex]\mu_s[/katex]) is usually greater than kinetic friction ([katex]\mu_k[/katex]) as it resists the start of motion. |
| [katex]k[/katex] | Spring constant, in [katex]\text{N/m}[/katex] |
| [katex] M_E = 5.972 \times 10^{24} , \text{kg} [/katex] | Mass of the Earth |
| [katex] M_M = 7.348 \times 10^{22} , \text{kg} [/katex] | Mass of the Moon |
| [katex] M_M = 1.989 \times 10^{30} , \text{kg} [/katex] | Mass of the Sun |
| Variable | SI Unit |
|---|---|
| [katex]s[/katex] (Displacement) | [katex]\text{meters (m)}[/katex] |
| [katex]v[/katex] (Velocity) | [katex]\text{meters per second (m/s)}[/katex] |
| [katex]a[/katex] (Acceleration) | [katex]\text{meters per second squared (m/s}^2\text{)}[/katex] |
| [katex]t[/katex] (Time) | [katex]\text{seconds (s)}[/katex] |
| [katex]m[/katex] (Mass) | [katex]\text{kilograms (kg)}[/katex] |
| Variable | Derived SI Unit |
|---|---|
| [katex]F[/katex] (Force) | [katex]\text{newtons (N)}[/katex] |
| [katex]E[/katex], [katex]PE[/katex], [katex]KE[/katex] (Energy, Potential Energy, Kinetic Energy) | [katex]\text{joules (J)}[/katex] |
| [katex]P[/katex] (Power) | [katex]\text{watts (W)}[/katex] |
| [katex]p[/katex] (Momentum) | [katex]\text{kilogram meters per second (kgm/s)}[/katex] |
| [katex]\omega[/katex] (Angular Velocity) | [katex]\text{radians per second (rad/s)}[/katex] |
| [katex]\tau[/katex] (Torque) | [katex]\text{newton meters (Nm)}[/katex] |
| [katex]I[/katex] (Moment of Inertia) | [katex]\text{kilogram meter squared (kgm}^2\text{)}[/katex] |
| [katex]f[/katex] (Frequency) | [katex]\text{hertz (Hz)}[/katex] |
Metric Prefixes
Example of using unit analysis: Convert 5 kilometers to millimeters.
Start with the given measurement: [katex]\text{5 km}[/katex]
Use the conversion factors for kilometers to meters and meters to millimeters: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}}[/katex]
Perform the multiplication: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}} = 5 \times 10^3 \times 10^3 \, \text{mm}[/katex]
Simplify to get the final answer: [katex]\boxed{5 \times 10^6 \, \text{mm}}[/katex]
Prefix | Symbol | Power of Ten | Equivalent |
|---|---|---|---|
Pico- | p | [katex]10^{-12}[/katex] | |
Nano- | n | [katex]10^{-9}[/katex] | |
Micro- | µ | [katex]10^{-6}[/katex] | |
Milli- | m | [katex]10^{-3}[/katex] | |
Centi- | c | [katex]10^{-2}[/katex] | |
Deci- | d | [katex]10^{-1}[/katex] | |
(Base unit) | – | [katex]10^{0}[/katex] | |
Deca- or Deka- | da | [katex]10^{1}[/katex] | |
Hecto- | h | [katex]10^{2}[/katex] | |
Kilo- | k | [katex]10^{3}[/katex] | |
Mega- | M | [katex]10^{6}[/katex] | |
Giga- | G | [katex]10^{9}[/katex] | |
Tera- | T | [katex]10^{12}[/katex] |
One price to unlock most advanced version of Phy across all our tools.
per month
Billed Monthly. Cancel Anytime.
We crafted THE Ultimate A.P Physics 1 Program so you can learn faster and score higher.
Try our free calculator to see what you need to get a 5 on the 2026 AP Physics 1 exam.
Understand you mistakes quicker.
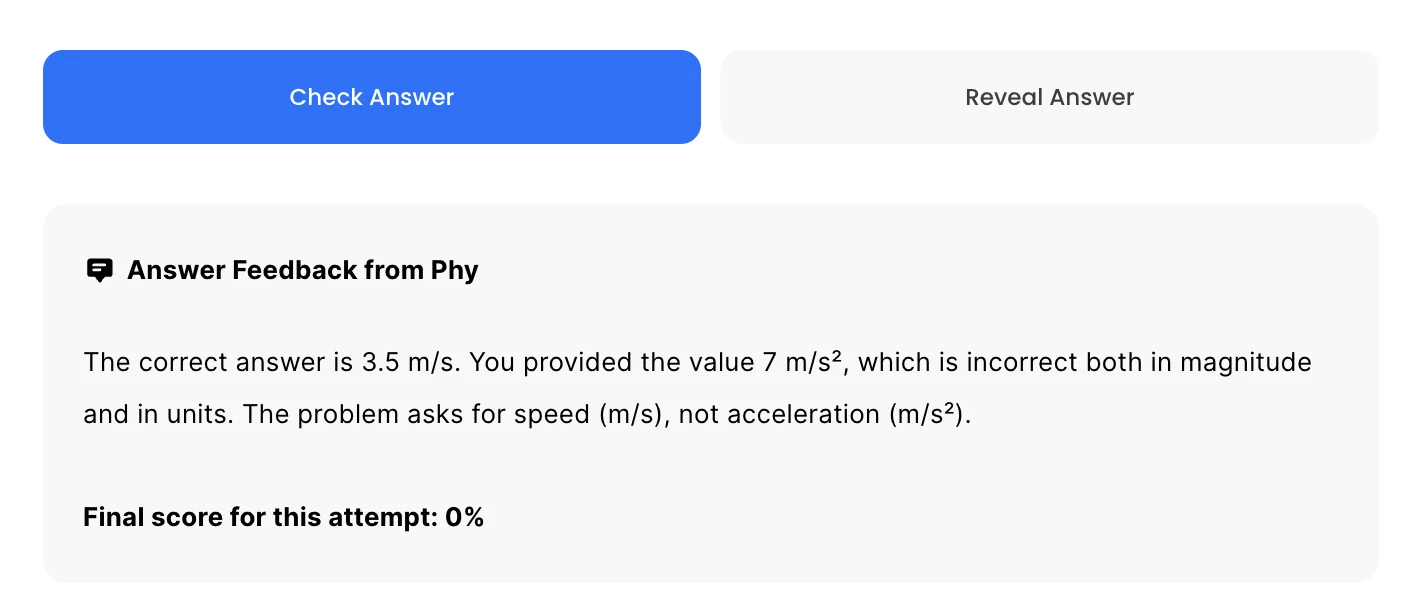
Phy automatically provides feedback so you can improve your responses.
10 Free Credits To Get You Started
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.
Feeling uneasy about your next physics test? We'll boost your grade in 3 lessons or less—guaranteed
