0 attempts
0% avg
UBQ Credits
First, convert the rotational speed to radians per second: [katex]\omega = 45 , \frac{\text{rev}}{\text{min}} \times \frac{1 , \text{min}}{60 , \text{s}} \times \frac{2\pi , \text{radians}}{1 , \text{rev}}[/katex].
Note you can convert to linear velocity [katex] v [/katex] instead of using [katex] \omega [/katex], since [katex] v = \omega r [/katex], where [katex] r [/katex] is the radius of the circle.
The minimum coefficient of static friction is found using the balance of forces in the vertical direction, with the static frictional force providing the upward force to counteract gravity, and the centripetal force being provided by the normal force.
| Step | Formula / Derivation | Reasoning |
|---|---|---|
| 1 | [katex]a_c = \frac{v^2}{R}[/katex] | Centripetal acceleration formula. |
| 2 | [katex]v = R\omega[/katex] | Linear velocity in terms of radius and angular velocity. |
| 3 | [katex]a_c = R\omega^2[/katex] | Substitute [katex]v[/katex] into the centripetal acceleration formula. |
| 4 | [katex]F_c = m a_c = m R\omega^2[/katex] | Centripetal force provided by the normal force. |
| 5 | [katex]f_s = \mu_s N[/katex] | Static frictional force opposing gravity. |
| 6 | [katex]f_s = m g[/katex] | Static frictional force equals gravitational force to prevent sliding. |
| 7 | [katex]\mu_s = \frac{f_s}{N} = \frac{mg}{mR\omega^2}[/katex] | Substitute [katex]f_s[/katex] and [katex]N[/katex] with their equivalents. |
| 8 | [katex]\mu_s = \frac{g}{R\omega^2}[/katex] | Cancel [katex]m[/katex] from the equation. |
| 9 | [katex]\mu_s = \frac{g}{R\left(\frac{45}{60} \times 2\pi\right)^2}[/katex] | Substitute [katex]\omega[/katex] with its value in terms of rev/min to rad/s. |
| 10 | [katex]\mu_s = \frac{9.8}{4\left(\frac{3}{4} \pi\right)^2}[/katex] | Substitute given values for [katex]g[/katex] and [katex]R[/katex]. |
| 11 | [katex]\mu_s = \frac{9.8}{4\left(\frac{9}{16} \pi^2\right)}[/katex] | Simplify the expression for [katex]\omega^2[/katex]. |
| 12 | [katex]\boxed{\mu_s = \frac{9.8 \times 16}{4 \times 9 \pi^2}}[/katex] | Final expression for [katex]\mu_s[/katex]. |
Now let’s calculate the exact value for the minimum coefficient of static friction required.
The minimum coefficient of static friction required so that the rider does not slide down the wall is [katex] \boxed{\mu_s \approx 0.11} [/katex]
Just ask: "Help me solve this problem."
A 2 kg ball is swung in a vertical circle. The length of the string the ball is attached to is 0.7 m. It takes 0.4 s for the ball to travel one revolution ( assume ball travels at constant speed).
The International Space Station has a mass of 4.2 x105 kg and orbits Earth at a distance of 4.0 x102 km above the surface. Earth has a radius of 6.37 x106 m, and mass of 5.97 x1024 kg. Calculate the following:
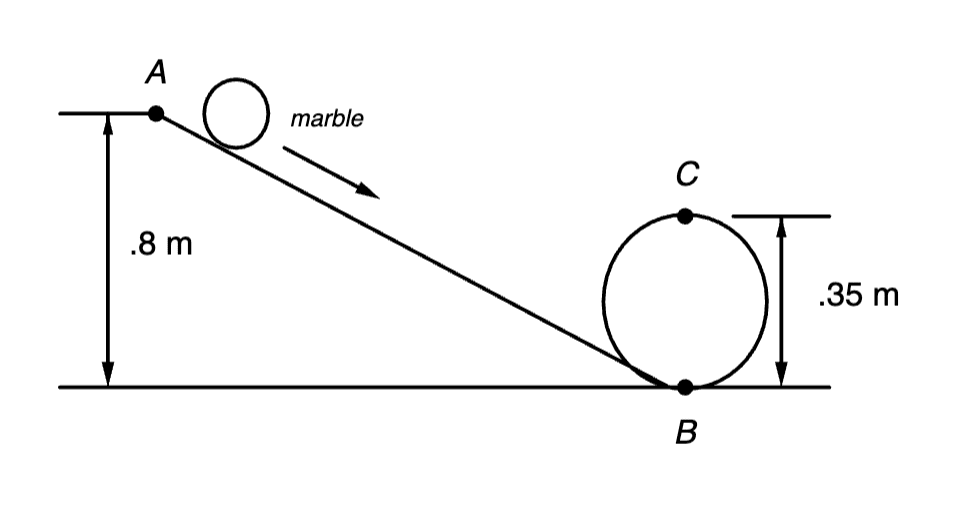
The diagram above shows a marble rolling down an incline, the bottom part of which has been bent into a loop. The marble is released from point A at a height of 0.80 m above the ground. Point B is the lowest point and point C the highest point of the loop. The diameter of the loop is 0.35 m. The mass of the marble is 0.050 kg. Friction forces and any gain in kinetic energy due to the rotating of the marble can be ignored. When answering the following questions, consider the marble when it is at point C.
A discus is held at the end of an arm that starts at rest. The average angular acceleration of [katex]54 \, \text{rad/s}^2 [/katex] lasts for 0.25 s. The path is circular and has radius 1.1 m.
Note: A discuss is a heavy, flattened circular object for throwing.
A rock is whirled on the end of a string in a horizontal circle of radius R with a constant period T. If the radius of the circle is reduced to R/3, while the period remains T, what happens to the centripetal acceleration (ac) of the rock?
[katex] \boxed{\mu_s \approx 0.11} [/katex]
By continuing you (1) agree to our Terms of Sale and Terms of Use and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
| Kinematics | Forces |
|---|---|
| \(\Delta x = v_i t + \frac{1}{2} at^2\) | \(F = ma\) |
| \(v = v_i + at\) | \(F_g = \frac{G m_1 m_2}{r^2}\) |
| \(v^2 = v_i^2 + 2a \Delta x\) | \(f = \mu N\) |
| \(\Delta x = \frac{v_i + v}{2} t\) | \(F_s =-kx\) |
| \(v^2 = v_f^2 \,-\, 2a \Delta x\) |
| Circular Motion | Energy |
|---|---|
| \(F_c = \frac{mv^2}{r}\) | \(KE = \frac{1}{2} mv^2\) |
| \(a_c = \frac{v^2}{r}\) | \(PE = mgh\) |
| \(T = 2\pi \sqrt{\frac{r}{g}}\) | \(KE_i + PE_i = KE_f + PE_f\) |
| \(W = Fd \cos\theta\) |
| Momentum | Torque and Rotations |
|---|---|
| \(p = mv\) | \(\tau = r \cdot F \cdot \sin(\theta)\) |
| \(J = \Delta p\) | \(I = \sum mr^2\) |
| \(p_i = p_f\) | \(L = I \cdot \omega\) |
| Simple Harmonic Motion | Fluids |
|---|---|
| \(F = -kx\) | \(P = \frac{F}{A}\) |
| \(T = 2\pi \sqrt{\frac{l}{g}}\) | \(P_{\text{total}} = P_{\text{atm}} + \rho gh\) |
| \(T = 2\pi \sqrt{\frac{m}{k}}\) | \(Q = Av\) |
| \(x(t) = A \cos(\omega t + \phi)\) | \(F_b = \rho V g\) |
| \(a = -\omega^2 x\) | \(A_1v_1 = A_2v_2\) |
| Constant | Description |
|---|---|
| [katex]g[/katex] | Acceleration due to gravity, typically [katex]9.8 , \text{m/s}^2[/katex] on Earth’s surface |
| [katex]G[/katex] | Universal Gravitational Constant, [katex]6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2[/katex] |
| [katex]\mu_k[/katex] and [katex]\mu_s[/katex] | Coefficients of kinetic ([katex]\mu_k[/katex]) and static ([katex]\mu_s[/katex]) friction, dimensionless. Static friction ([katex]\mu_s[/katex]) is usually greater than kinetic friction ([katex]\mu_k[/katex]) as it resists the start of motion. |
| [katex]k[/katex] | Spring constant, in [katex]\text{N/m}[/katex] |
| [katex] M_E = 5.972 \times 10^{24} , \text{kg} [/katex] | Mass of the Earth |
| [katex] M_M = 7.348 \times 10^{22} , \text{kg} [/katex] | Mass of the Moon |
| [katex] M_M = 1.989 \times 10^{30} , \text{kg} [/katex] | Mass of the Sun |
| Variable | SI Unit |
|---|---|
| [katex]s[/katex] (Displacement) | [katex]\text{meters (m)}[/katex] |
| [katex]v[/katex] (Velocity) | [katex]\text{meters per second (m/s)}[/katex] |
| [katex]a[/katex] (Acceleration) | [katex]\text{meters per second squared (m/s}^2\text{)}[/katex] |
| [katex]t[/katex] (Time) | [katex]\text{seconds (s)}[/katex] |
| [katex]m[/katex] (Mass) | [katex]\text{kilograms (kg)}[/katex] |
| Variable | Derived SI Unit |
|---|---|
| [katex]F[/katex] (Force) | [katex]\text{newtons (N)}[/katex] |
| [katex]E[/katex], [katex]PE[/katex], [katex]KE[/katex] (Energy, Potential Energy, Kinetic Energy) | [katex]\text{joules (J)}[/katex] |
| [katex]P[/katex] (Power) | [katex]\text{watts (W)}[/katex] |
| [katex]p[/katex] (Momentum) | [katex]\text{kilogram meters per second (kgm/s)}[/katex] |
| [katex]\omega[/katex] (Angular Velocity) | [katex]\text{radians per second (rad/s)}[/katex] |
| [katex]\tau[/katex] (Torque) | [katex]\text{newton meters (Nm)}[/katex] |
| [katex]I[/katex] (Moment of Inertia) | [katex]\text{kilogram meter squared (kgm}^2\text{)}[/katex] |
| [katex]f[/katex] (Frequency) | [katex]\text{hertz (Hz)}[/katex] |
General Metric Conversion Chart
Example of using unit analysis: Convert 5 kilometers to millimeters.
Start with the given measurement: [katex]\text{5 km}[/katex]
Use the conversion factors for kilometers to meters and meters to millimeters: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}}[/katex]
Perform the multiplication: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}} = 5 \times 10^3 \times 10^3 \, \text{mm}[/katex]
Simplify to get the final answer: [katex]\boxed{5 \times 10^6 \, \text{mm}}[/katex]
Prefix | Symbol | Power of Ten | Equivalent |
|---|---|---|---|
Pico- | p | [katex]10^{-12}[/katex] | 0.000000000001 |
Nano- | n | [katex]10^{-9}[/katex] | 0.000000001 |
Micro- | µ | [katex]10^{-6}[/katex] | 0.000001 |
Milli- | m | [katex]10^{-3}[/katex] | 0.001 |
Centi- | c | [katex]10^{-2}[/katex] | 0.01 |
Deci- | d | [katex]10^{-1}[/katex] | 0.1 |
(Base unit) | – | [katex]10^{0}[/katex] | 1 |
Deca- or Deka- | da | [katex]10^{1}[/katex] | 10 |
Hecto- | h | [katex]10^{2}[/katex] | 100 |
Kilo- | k | [katex]10^{3}[/katex] | 1,000 |
Mega- | M | [katex]10^{6}[/katex] | 1,000,000 |
Giga- | G | [katex]10^{9}[/katex] | 1,000,000,000 |
Tera- | T | [katex]10^{12}[/katex] | 1,000,000,000,000 |
The most advanced version of Phy. 50% off, for early supporters. Prices increase soon.
per month
Billed Monthly. Cancel Anytime.
Trial –> Phy Pro
A quick explanation
Credits are used to grade your FRQs and GQs. Pro users get unlimited credits.
Submitting counts as 1 attempt.
Viewing answers or explanations count as a failed attempts.
Phy gives partial credit if needed
MCQs and GQs are are 1 point each. FRQs will state points for each part.
Phy customizes problem explanations based on what you struggle with. Just hit the explanation button to see.
Understand you mistakes quicker.
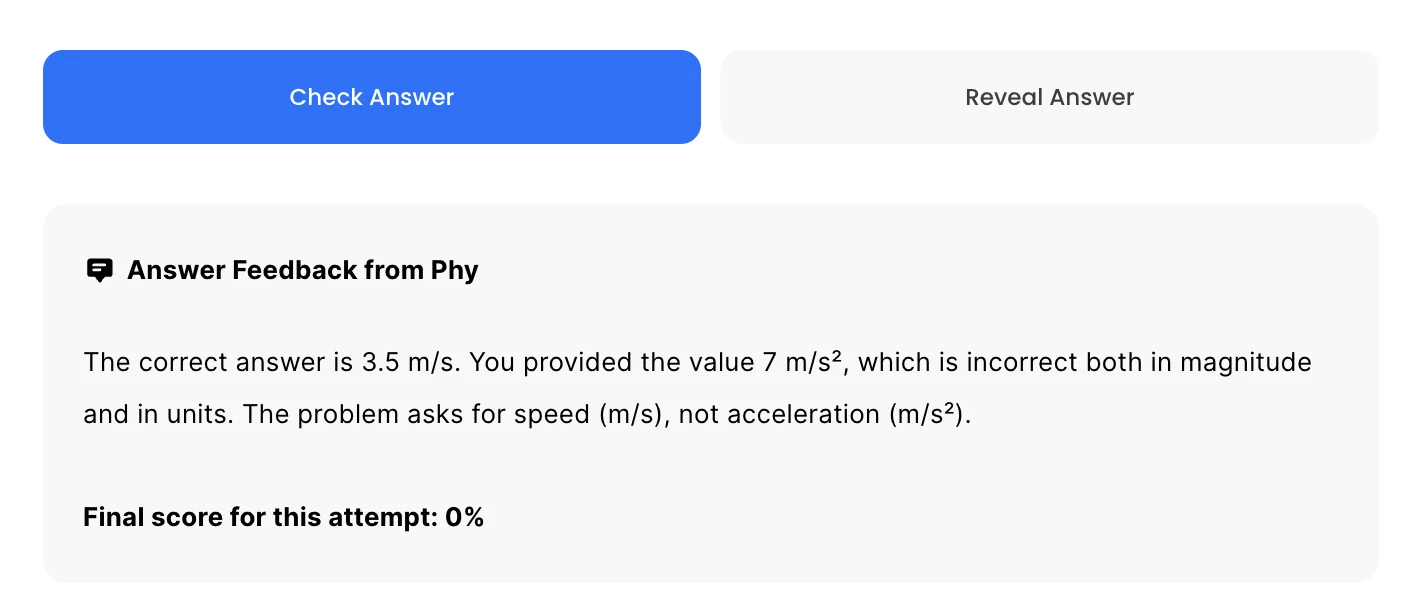
Phy automatically provides feedback so you can improve your responses.
10 Free Credits To Get You Started
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.