0 attempts
0% avg
UBQ Credits
Part A – Minimum work required
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | \[\Delta x = 35\,\text{m} + 50\,\text{m} = 85\,\text{m}\] | The water is pumped from the bottom of the well (35 m deep) to a house 50 m above the well; hence the total vertical displacement is \(85\,\text{m}\). |
| 2 | \[W = \rho\,V\,g\,\Delta x\] | This formula gives the gravitational work (or potential energy gain) required to move a volume \(V\) of water with density \(\rho\) against gravity \(g\) through a vertical displacement \(\Delta x\). |
| 3 | \[W = (1000\,\text{kg/m}^3)(0.35\,\text{m}^3)(9.8\,\text{m/s}^2)(85\,\text{m})\] | Substitute the numerical values: water density \(\rho = 1000\,\text{kg/m}^3\), volume \(V = 0.35\,\text{m}^3\), gravitational acceleration \(g = 9.8\,\text{m/s}^2\), and displacement \(\Delta x = 85\,\text{m}\). |
| 4 | \[W \approx 2.92 \times 10^5\,\text{J}\] | Performing the multiplication gives \(W \approx 291550\,\text{J}\), which is rounded to \(2.92 \times 10^5\,\text{J}\). |
| 5 | \[\boxed{W \approx 2.92 \times 10^5\,\text{J}}\] | This is the minimum work required to pump the water used per day. |
Part B – Minimum power rating
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | \[t = 2\,\text{hours} = 7200\,\text{s}\] | Convert the pumping time from hours to seconds for consistency in SI units. |
| 2 | \[P = \frac{W}{t}\] | Power is defined as the work done per unit time. |
| 3 | \[P = \frac{2.92 \times 10^5\,\text{J}}{7200\,\text{s}} \approx 40.5\,\text{W}\] | Substitute the work calculated in part (a) and the conversion for time to find the minimum power rating of the pump. |
| 4 | \[\boxed{P \approx 40.5\,\text{W}}\] | This represents the minimum power needed to pump the water within the specified time. |
Part C – Flow velocity
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | \[A_{\text{well}} = \frac{\pi (0.03)^2}{4}\] | Calculate the cross-sectional area of the pipe in the well (pipe diameter = 3.0 cm = 0.03 m). |
| 2 | \[Q = A_{\text{well}}\,v_i\] | The volumetric flow rate \(Q\) in the well is the product of the area and the well velocity \(v_i = 0.50\,\text{m/s}\). |
| 3 | \[A_{\text{house}} = \frac{\pi (0.0125)^2}{4}\] | Calculate the cross-sectional area of the pipe at the house (pipe diameter = 1.25 cm = 0.0125 m). |
| 4 | \[A_{\text{well}}\,v_i = A_{\text{house}}\,v_x \quad \Rightarrow \quad v_x = \frac{A_{\text{well}}}{A_{\text{house}}}\,v_i\] | Using mass continuity (volume flow rate is constant), relate the velocity in the well \(v_i\) to the velocity in the house \(v_x\) via their cross-sectional areas. |
| 5 | \[\frac{A_{\text{well}}}{A_{\text{house}}} = \left(\frac{0.03}{0.0125}\right)^2 = (2.4)^2 = 5.76\] | Since both areas involve the factor \(\pi/4\), the ratio simplifies to the square of the ratio of the diameters. |
| 6 | \[v_x = 5.76 \times 0.50 = 2.88\,\text{m/s}\] | Multiply the well velocity by the area ratio to obtain the flow velocity at the house’s faucet. |
| 7 | \[\boxed{v_x \approx 2.88\,\text{m/s}}\] | This is the calculated flow velocity when the faucet in the house is open. |
Part D – Calculating minimum pressure
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | \[\text{Energy per unit volume: } \Delta P = \rho g\,\Delta x + \frac{1}{2}\rho\,(v_x^2 – v_i^2)\] | This expression (derived from Bernoulli’s principle) represents the pressure energy per unit volume needed to overcome both the gravitational potential \(\rho g\,\Delta x\) and to provide the increase in kinetic energy from \(v_i\) (in the well) to \(v_x\) (at the faucet). |
| 2 | \[P_{\text{faucet, min}} = \rho g\,\Delta x + \frac{1}{2}\rho\,v_x^2\] | For minimum pressure at the faucet (assuming negligible initial kinetic energy \(v_i \approx 0\) or that its contribution is already included in the pump pressure), the faucet must supply at least the hydrostatic pressure plus the dynamic pressure necessary for the flow velocity \(v_x\). In practice, if the faucet discharges to the atmosphere, its gauge pressure is 0, so the pump must overcome this total pressure drop. |
| 3 | \[\boxed{P_{\text{min at faucet}} = \rho g\,\Delta x + \frac{1}{2}\rho\,v_x^2}\] | This is how one would calculate the minimum pressure required at the faucet: by summing the pressure needed to lift the water \(\rho g\,\Delta x\) and the pressure needed to accelerate it to \(v_x\) (i.e., \(\frac{1}{2}\rho\,v_x^2\)). |
| 4 | N/A | In summary, to find the minimum pressure at the faucet, you equate the pressure energy per unit volume provided by the pump with the sum of the gravitational and dynamic energy per unit volume required for the water to reach the faucet at velocity \(v_x\). This is essentially an algebraic application of Bernoulli’s principle under ideal (lossless) conditions. |
Just ask: "Help me solve this problem."
The diagram above shows a hydraulic chamber with a spring \( (k_s = 1250 \, \text{N/m}) \) attached to the input piston and a rock of mass \( 55.2 \, \text{kg} \) resting on the output plunger. The input piston and output plunger are at about the same height, and each has negligible mass. The chamber is filled with water.
The launching mechanism of a toy gun consists of a spring with an unknown spring constant, \( k \). When the spring is compressed \( 0.120 \, \text{m} \) vertically, a \( 35.0 \, \text{g} \) projectile is able to be fired to a maximum height of \( 25 \, \text{m} \) above the position of the projectile when the spring is compressed. Assume that the barrel of the gun is frictionless.
A bullet at speed [katex] v_0 [/katex] trikes and embeds itself in a block of wood which is suspended by a string, causing the bullet and block to rise to a maximum height h. Which of the following statements is true?
A fluid flows through the two sections of cylindrical pipe shown in the figure. The narrow section of the pipe has radius \( R \) and the wide section has radius \( 2R \). What is the ratio of the fluid’s speed in the wide section of pipe to its speed in the narrow section of pipe, \( \frac{v_{\text{wide}}}{v_{\text{narrow}}} \)?
A ski lift carries skiers along a \(695 \, \text{m}\) slope inclined at \(34^\circ\). To lift a single rider, it is necessary to move \(72 \, \text{kg}\) of mass to the top of the lift. Under maximum load conditions, five riders per minute arrive at the top. If \(65\%\) of the energy supplied by the motor goes to overcoming friction, what average power must the motor supply?
By continuing you (1) agree to our Terms of Use and Terms of Sale and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
| Kinematics | Forces |
|---|---|
| \(\Delta x = v_i t + \frac{1}{2} at^2\) | \(F = ma\) |
| \(v = v_i + at\) | \(F_g = \frac{G m_1 m_2}{r^2}\) |
| \(v^2 = v_i^2 + 2a \Delta x\) | \(f = \mu N\) |
| \(\Delta x = \frac{v_i + v}{2} t\) | \(F_s =-kx\) |
| \(v^2 = v_f^2 \,-\, 2a \Delta x\) |
| Circular Motion | Energy |
|---|---|
| \(F_c = \frac{mv^2}{r}\) | \(KE = \frac{1}{2} mv^2\) |
| \(a_c = \frac{v^2}{r}\) | \(PE = mgh\) |
| \(T = 2\pi \sqrt{\frac{r}{g}}\) | \(KE_i + PE_i = KE_f + PE_f\) |
| \(W = Fd \cos\theta\) |
| Momentum | Torque and Rotations |
|---|---|
| \(p = mv\) | \(\tau = r \cdot F \cdot \sin(\theta)\) |
| \(J = \Delta p\) | \(I = \sum mr^2\) |
| \(p_i = p_f\) | \(L = I \cdot \omega\) |
| Simple Harmonic Motion | Fluids |
|---|---|
| \(F = -kx\) | \(P = \frac{F}{A}\) |
| \(T = 2\pi \sqrt{\frac{l}{g}}\) | \(P_{\text{total}} = P_{\text{atm}} + \rho gh\) |
| \(T = 2\pi \sqrt{\frac{m}{k}}\) | \(Q = Av\) |
| \(x(t) = A \cos(\omega t + \phi)\) | \(F_b = \rho V g\) |
| \(a = -\omega^2 x\) | \(A_1v_1 = A_2v_2\) |
| Constant | Description |
|---|---|
| [katex]g[/katex] | Acceleration due to gravity, typically [katex]9.8 , \text{m/s}^2[/katex] on Earth’s surface |
| [katex]G[/katex] | Universal Gravitational Constant, [katex]6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2[/katex] |
| [katex]\mu_k[/katex] and [katex]\mu_s[/katex] | Coefficients of kinetic ([katex]\mu_k[/katex]) and static ([katex]\mu_s[/katex]) friction, dimensionless. Static friction ([katex]\mu_s[/katex]) is usually greater than kinetic friction ([katex]\mu_k[/katex]) as it resists the start of motion. |
| [katex]k[/katex] | Spring constant, in [katex]\text{N/m}[/katex] |
| [katex] M_E = 5.972 \times 10^{24} , \text{kg} [/katex] | Mass of the Earth |
| [katex] M_M = 7.348 \times 10^{22} , \text{kg} [/katex] | Mass of the Moon |
| [katex] M_M = 1.989 \times 10^{30} , \text{kg} [/katex] | Mass of the Sun |
| Variable | SI Unit |
|---|---|
| [katex]s[/katex] (Displacement) | [katex]\text{meters (m)}[/katex] |
| [katex]v[/katex] (Velocity) | [katex]\text{meters per second (m/s)}[/katex] |
| [katex]a[/katex] (Acceleration) | [katex]\text{meters per second squared (m/s}^2\text{)}[/katex] |
| [katex]t[/katex] (Time) | [katex]\text{seconds (s)}[/katex] |
| [katex]m[/katex] (Mass) | [katex]\text{kilograms (kg)}[/katex] |
| Variable | Derived SI Unit |
|---|---|
| [katex]F[/katex] (Force) | [katex]\text{newtons (N)}[/katex] |
| [katex]E[/katex], [katex]PE[/katex], [katex]KE[/katex] (Energy, Potential Energy, Kinetic Energy) | [katex]\text{joules (J)}[/katex] |
| [katex]P[/katex] (Power) | [katex]\text{watts (W)}[/katex] |
| [katex]p[/katex] (Momentum) | [katex]\text{kilogram meters per second (kgm/s)}[/katex] |
| [katex]\omega[/katex] (Angular Velocity) | [katex]\text{radians per second (rad/s)}[/katex] |
| [katex]\tau[/katex] (Torque) | [katex]\text{newton meters (Nm)}[/katex] |
| [katex]I[/katex] (Moment of Inertia) | [katex]\text{kilogram meter squared (kgm}^2\text{)}[/katex] |
| [katex]f[/katex] (Frequency) | [katex]\text{hertz (Hz)}[/katex] |
General Metric Conversion Chart
Example of using unit analysis: Convert 5 kilometers to millimeters.
Start with the given measurement: [katex]\text{5 km}[/katex]
Use the conversion factors for kilometers to meters and meters to millimeters: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}}[/katex]
Perform the multiplication: [katex]\text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}} = 5 \times 10^3 \times 10^3 \, \text{mm}[/katex]
Simplify to get the final answer: [katex]\boxed{5 \times 10^6 \, \text{mm}}[/katex]
Prefix | Symbol | Power of Ten | Equivalent |
|---|---|---|---|
Pico- | p | [katex]10^{-12}[/katex] | |
Nano- | n | [katex]10^{-9}[/katex] | |
Micro- | µ | [katex]10^{-6}[/katex] | |
Milli- | m | [katex]10^{-3}[/katex] | |
Centi- | c | [katex]10^{-2}[/katex] | |
Deci- | d | [katex]10^{-1}[/katex] | |
(Base unit) | – | [katex]10^{0}[/katex] | |
Deca- or Deka- | da | [katex]10^{1}[/katex] | |
Hecto- | h | [katex]10^{2}[/katex] | |
Kilo- | k | [katex]10^{3}[/katex] | |
Mega- | M | [katex]10^{6}[/katex] | |
Giga- | G | [katex]10^{9}[/katex] | |
Tera- | T | [katex]10^{12}[/katex] |
The most advanced version of Phy. 50% off, for early supporters. Prices increase soon.
per month
Billed Monthly. Cancel Anytime.
Trial –> Phy Pro
We crafted THE Ultimate A.P Physics 1 course so you can learn faster and score higher.
Try our free calculator to see what you need to get a 5 on the upcoming AP Physics 1 exam.
Understand you mistakes quicker.
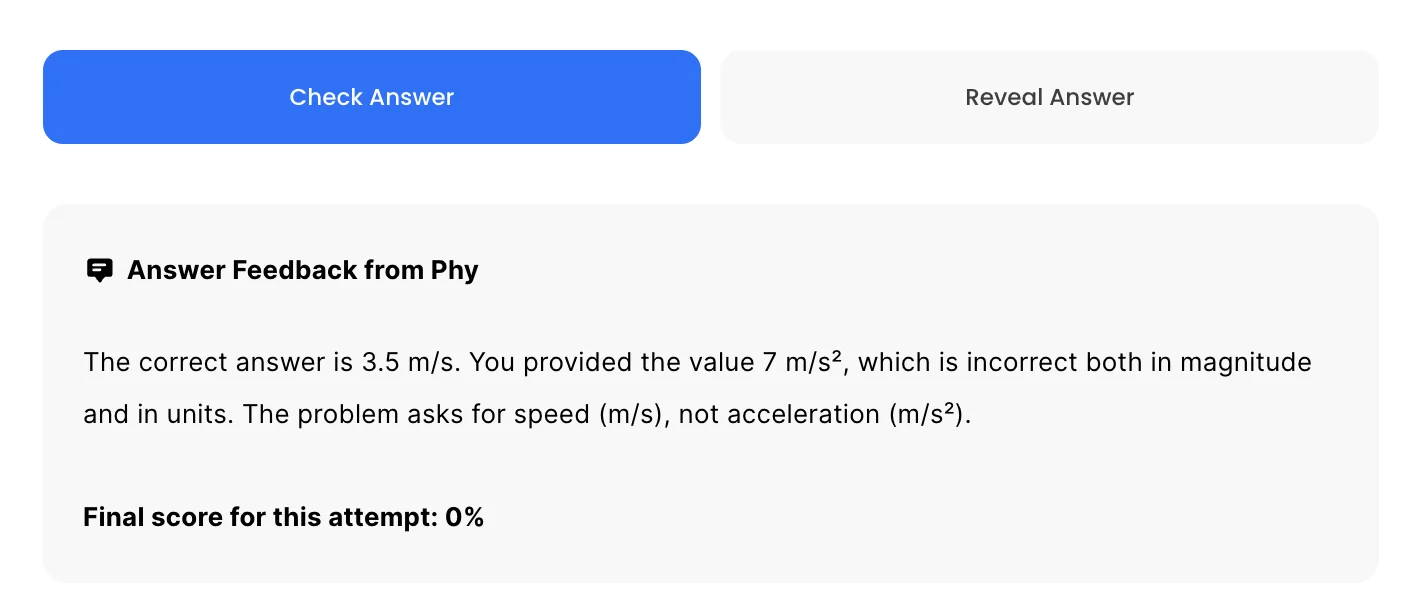
Phy automatically provides feedback so you can improve your responses.
10 Free Credits To Get You Started
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.
