Concept Overview
- Kinematic variables: displacement, distance, velocity, speed, acceleration, and time.
- Kinematic Equations
- Average speed vs average velocity
- Motion in one dimension – cars, balls, and any object moving in one direction
- Motion in two dimensions – object dropped from a moving plane, a bullet fired horizontally, balled kicked at 45°, and all types of projectile motion.
- Graphs: displacement vs time, velocity vs time, acceleration vs time.
Kinematic Variables
There are 5 total kinematic variables: ∆x, v0, vf, a, t.
Velocity (v) is split into two variables: Final Velocity (vf) and Initial Velocity (v0).
Time is measured in second and doesn’t have a direction.
Now let’s cover some misconception.
Displacement (∆x)
Displacement (a vector quantity) is how far an object has moved from its origin. Distance (a scalar quantity) is the total amount traveled.
Suppose you took a 200-mile trip to LA and back. Your displacement is zero (because you’re back where you started). Your distance, however, is 400 miles (200 miles to and 200 miles back)
Velocity (v0 and vf)
Velocity (a vector quantity) is how fast displacement changes. Speed is how fast distance changes.
Suppose you run 1 lap around a 100 meter track in 100 seconds. Your speed is 1 m/s. And your velocity is 0 m/s.
Acceleration (a)
Acceleration (a vector quantity) is how fast velocity changes. Think of you speeding up or slowing down in your car. An acceleration can also be caused by a change in direction. Kinematics ONLY deals with uniform (constant) acceleration. Non-uniform acceleration requires calculus.
Suppose you drop a ball from a tall building. How fast is it traveling after 3 seconds?
Since the ball accelerates due to gravity at 9.81 m/s2, this means that every second the ball gains 9.81 m/s of speed. So after 3 seconds it reaches a speed of 29.4 m/s.
Time (a scalar quantity) is often overlooked. It’s the key to solving many projectile motion (2 dimensional) problems. Why?
Because time is the SAME in the X and Y direction (more on why this matters below).
Kinematic Equations
Couple of things to remember regarding variable notation:
- ∆ = delta. It means “change in,” which literally means “final – initial.”
- s = distance. ∆x = change in horizontal displacement. ∆y = change in vertical displacement
- vo = initial velocity. It is pronounced “V knot.”
- Equations apply both horizontally and vertically
- Use subscripts in the equations to keep track of direction. For example, initial velocity in the vertical direction can be written as, “voy“. Displacement in the vertical direction can be written as ∆y.
Memorize
Memorizing the big 4 kinematic equations goes a long way. It only takes around 10 minutes.
Students that have memorized the formulas, can solve kinematic problems 30-50% faster than students that haven’t.
The best way to memorize is to write them down on a flashcard and practice 20 kinematic problems.
Here are the big 4 kinematic equations:
- v_f = v_0 +at
- v_f^2 = v_0^2 + 2a\Delta x
- \Delta x = v_0^2 + \frac{1}{2}at^2
- \Delta x = \frac{1}{2} t (v_f + v_0)
Average Speed vs Average Velocity
While we already covered velocity above, this topic seems to confuse students a bit. So here’s a more in depth explanation.
There is big difference between average speed and velocity.
Average speed is distance divided by time: speed = \frac{d}{t} .
Average velocity is displacement divided by time: \overline{v} = \frac{\Delta x}{\Delta t} .
Example: suppose you run 100 meters north, then back 100 m south, in 100 seconds. Using the equations from above we can find that
a) your average speed is = 200 m ÷ 100s = 2 m/s
b) your average velocity is 0m ÷ 100s = 0m/sec. (Remember that displacement is 0, since you end back up at your starting position)
Motion in 1-Dimension
Any object moving in a straight line ( up, down, left, right ) is moving in one direction. A car that starts from rest and accelerates to 80 m/s in 30 seconds, is moving in one direction.
Let’s say we are asked to find the distance the car traveled in 30 seconds. Start by choosing a kinematic equation that has all the given variables, then plug the numbers in. It’s as simple as that!
Picking the Right Equation
Here’s a little trick if you can’t figure out what equation to use:
There are no more than four variables in each kinematic equation. Similarly, every kinematics problem has four variables: three known and one unknown variable)
Write out the 4 variables and see which kinematic equation has all 4. In the example above we have: vo , vf , t , and ∆x. Thus you should use the equation: \Delta x = \frac{1}{2} t (v_f + v_0) .
Motion in 2-Dimensions
Objects moving in 2-dimensions, are moving both horizontally and vertically. These objects are called projectiles. Solve problems the exact same way as with one-dimensional kinematics, except apply the formulas in both directions.
Helpful Tips to Remember
- Time stays the same in both the x and y directions
- Horizontal speed, distance, or time, can be found using ∆x = vt
- The vertical acceleration is almost always, acceleration due to gravity (9.81 m/s)
- Unless given, the initial velocity is almost always 0.
- Vertical velocity at the top of the trajectory is always 0, but horizontal velocity remains constant.
- If a projectile is traveling at an initial angle, use trig to split the vector into horizontal and vertical components.
- The final velocity of the object is the SUM of the horizontal and vertical components of velocity
Solving 2d Motion Problems (Example)
A bullet shot horizontally at 90 m/s, from a height of 3.2 meters. Find how far the bullet travels.
To solve this problem just figure out what’s given in the horizontal and vertical directions, and pick a kinematic equation to solve for the unknown. Here’s an example of what the work might look like:
| Horizontal Components | Vertical Components |
|---|---|
| vox = 90 m/s | voy = 0 m/s |
| t =? | ay = 9.81 m/s2 |
| ∆x =? | ∆y = 3.2 m |
| t =? |
Hopefully, you can see the pattern here. We aren’t given enough information in the horizontal direction. Therefore, we will use a kinematic equation in the vertical direction to find the time.
Remember that time is the common factor in both directions. If we solve for t, we will be able to solve for the distance the bullet travels with the equation \Delta x = v_{0x} t .
Motion Graphs
Most students overlook graphing. It comes up quite a bit on the AP Exam. I’ll show you the best way to understand how these graphs work. First lets try a problem:
From the acceleration-time graph below, find the total change in velocity in the first 3 seconds.
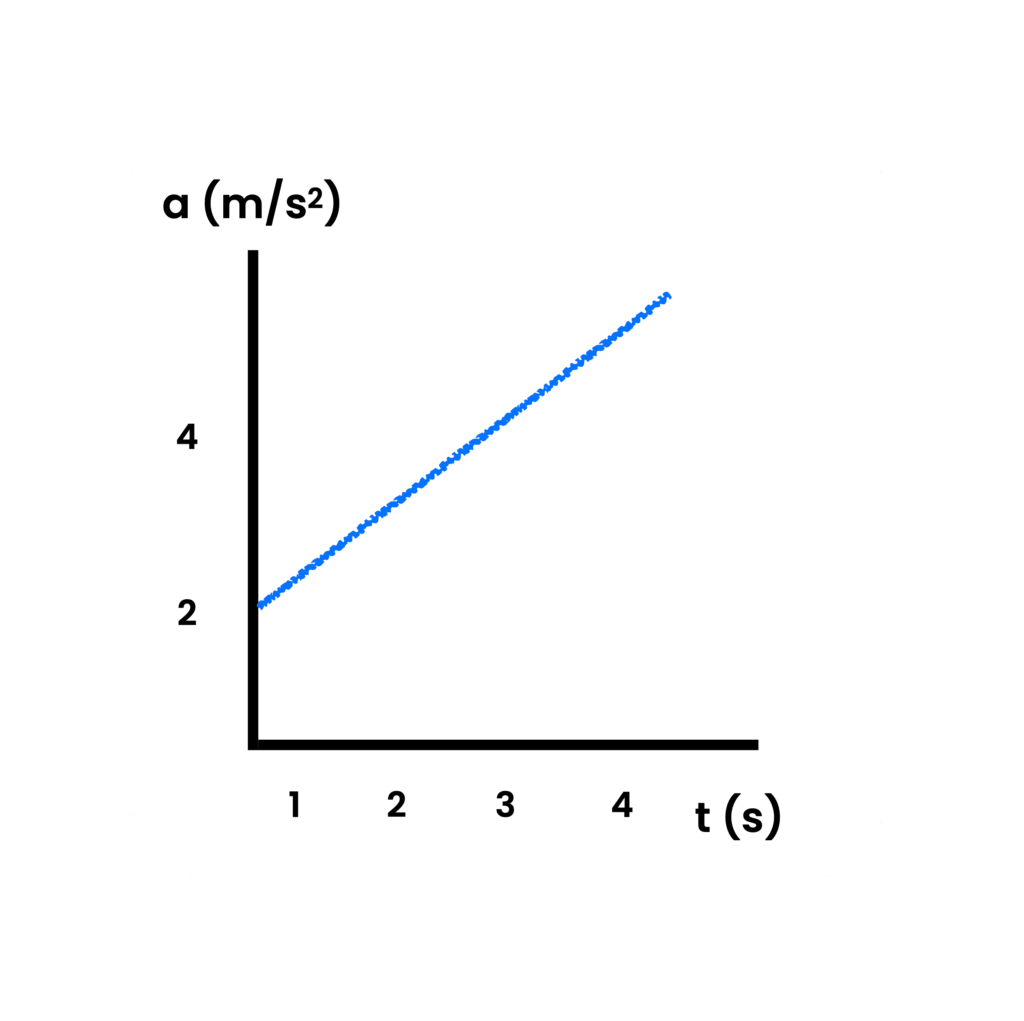
First, let’s take a step back and go back to definitions
- Velocity is the change in displacement per unit of time. “Change in” is another word for slope/derivative! Thus the slope of the displacement vs time graph is velocity!
- Acceleration is the change in velocity per unit of time. Thus the slope of the velocity vs time graph is acceleration.
Look at it like this: ∆x → ∆v → a. To get to the next one just find the slope/derivative!
Now go backwards: a → ∆v → ∆x. To get to the next one just find the opposite of the derivative: the integral (a fancy way of saying area under the curve!)
Are you able to solve the problem above now? If you are, great job! Keep practicing with the problems at the end of this post!
Practice Questions for Mastery
Solve all 8 questions and write down your answers. Solutions are given below. Swipe horizontally to see the next question.
(1) The international space station travels at 7660 m/s. Find the average velocity of the space station, if it takes 90 minutes to make one full orbit around earth.
⇨ concepts involved: average velocity, problem-solving
⇨ difficulty: easy
(2) Police officers have measured the length of a car’s tire skid marks to be 23 meters. This particular car is known to decelerate at a constant 7.5 m/s2. What was the car’s initial velocity?
⇨ concepts involved: kinematic equations, problem-solving
⇨ difficulty: easy
(3) A plane, 220 meters high, is dropping a supply crate to an island below. It is traveling with a horizontal velocity of 150 m/s. At what horizontal distance must the plane drop the supply crate for it to land on the island?
(a) 589 meters (b) 755 meters (c) 964 meters (d) 1005 meters (e) 1127 meters
⇨ concepts involved: kinematics in two dimensions/projectiles, problem-solving logic
⇨ difficulty: medium
(4) A rock is thrown at an angle of 42° above the horizontal at a speed of 14 m/s. Determine how long it takes the rock to hit the ground.
(a) .92 seconds (b) 1.8 seconds (c) 2.4 seconds (d) 3.3 seconds (e) 3.9 seconds
⇨ concepts involved: projectile motion, problem-solving
⇨ difficulty: hard
(5) Conceptual problem: A golfer hits her ball in a high arcing shot. Air resistance is negligible. When the ball is at its highest point, which of the following is true?
(a) acceleration and velocity are both zero
(b) the ball has zero velocity for a split second
(c) the ball’s range is at a maximum
(d) both the x and y components of velocity are zero
(e) the x component of velocity is greater than the y component of velocity
⇨ concepts involved: projectile motion, range, vector components
⇨ difficulty: easy
(6) A soccer ball is kicked horizontally off an 85-meter high cliff, at a speed of 34 m/s. What was the ball’s final speed when it hit the ground below?
(a) 53 m/s (b) 41 m/s (c) 1681 m/s (d) 776 m/s (e) more information is needed
⇨ concepts involved: projectile motion, speed
⇨ difficulty: medium
(7) Conceptual Problem: A 100-pound rock and a 1-pound metal arrow pointed downwards, are dropped from height h. Assuming there is no air resistance, which one hits the ground first.
⇨ concepts involved: free-fall, acceleration, vertical kinematics
⇨ difficulty: medium
(8) A arrow is shot horizontally from a distance of 20 meters away. It lands .05 meters below the center of the target. If air resistance is negligible what was the initial speed of the arrow?
⇨ concepts involved: projectile motion, speed
⇨ difficulty: medium
Challenge Questions (Bonus)
These are much harder questions, typically seen on an AP Exam.
(1) A gun can fire a bullet to height h when fired straight up. If the same gun is pointed at an angle of 45° from the vertical, what is the new maximum height of the projectile?
(a) h/4
(b) h/(2√2)
(c) h/2
(d) h/√2
(e) h
⇨ concepts involved: free-fall, projectile motion, problem-solving
⇨ difficulty: medium
(2) Conceptual Problem: Two balls are dropped off a cliff, 3 seconds apart. The first ball dropped is twice as heavy as the second ball dropped. Air resistance is negligible. While both balls are falling, the distance between the two balls is:
(a) constant
(b) increasing
(c) decreasing
(d) dependent on the height
(e) unknown
⇨ concepts involved: free-fall, projectile motion, acceleration due to gravity
⇨ difficulty: hard
Free Practice Tests
Here are some free kinematics practice test made by other sites! These are AP level questions.
- Test #1
- Test #2
- Test #3 (Beginner Level)
- Test #4 (AP Level)
- Test #5 (AP Level)
- Free Response Questions
Conclusion
Congrats! That wraps up everything you need to know for kinematics in both regular and advanced Physics classes.
It’s best to apply your knowledge to see if you really are understanding these concepts.
So if you are still having trouble answer these questions, try practicing more questions. Or try working with a teacher/professional physics mentor to iron out any misunderstanding.
Up next, we have a speed review for linear forces!
