A skier with a mass of \(58 \, \text{kg}\) glides up a snowy incline that forms an angle of \(28^\circ\) with the horizontal. The skier initially moves at a speed of \(7.2 \, \text{m/s}\). After traveling a distance of \(2.3 \, \text{m}\) up the slope, the skier’s speed reduces to \(3.8 \, \text{m/s}\).
A disk increases from 2 complete revolutions in 2 seconds to 5 complete revolutions in 2 seconds. What is its average angular acceleration?
Two uniform solid balls, one of radius \( R \) and mass \( M \), the other of radius \( 2R \) and mass \( 8M \), roll down a high incline. They start together from rest at the top of the incline. Which one will reach the bottom of the incline first?
A small boat coasts at constant speed under a bridge. A heavy sack of sand is dropped from the bridge onto the boat. The speed of the boat
A man weighing \( 700 \) \( \text{N} \) and a woman weighing \( 400 \) \( \text{N} \) have the same momentum. What is the ratio of the man’s kinetic energy \( K_m \) to that of the woman \( K_w \)?
A person is trying to judge whether a picture (mass = 1.42 kg) is properly positioned by temporarily pressing it against a wall. The pressing force is perpendicular to the wall. The coefficient of static friction between the picture and the wall is 0.62. What is the minimum amount of pressing force that must be used?
A child has a toy tied to the end of a string and whirls the toy at constant speed in a horizontal circular path of radius \(R\). The toy completes each revolution of its motion in a time period \(T\). What is the magnitude of the acceleration of the toy (in terms of \(T\), \(R\), and \(g\))?
A pulley has an initial angular speed of \( 12.5 \) \( \text{rad/s} \) and a constant angular acceleration of \( 3.41 \) \( \text{rad/s}^2 \). Through what angle does the pulley turn in \( 5.26 \) \( \text{s} \)?
If an object is moving, is it possible for the net force acting on it to be zero? Explain.
Which pair of quantities will always have the same magnitude if motion is in a straight line and in one direction?
A cube of side length \( s \) rests on the bottom surface of a container of fluid. The fluid is at a height \( y \) above the bottom of the tank. The fluid has density \( \rho \) and the atmospheric pressure is \( P_{\text{atm}} \).
Which of the following expressions is equal to the absolute pressure exerted by the fluid on the top surface of the cube?
A massless rigid rod of length [katex]3d[/katex] is pivoted at a fixed point [katex]W[/katex], and two forces each of magnitude [katex]F[/katex] are applied vertically upward as shown above. A third vertical force of magnitude [katex]F[/katex] may be applied, either upward or downward, at one of the labeled points. With the proper choice of direction at each point, the rod can be in equilibrium if the third force of magnitude [katex]F[/katex] is applied at point?
At time \( t = 0 \), an object is released from rest at position \( x = +x_{\text{max}} \) and undergoes simple harmonic motion along the \( x \)-axis about the equilibrium position of \( x = 0 \). The period of oscillation of the object is \( T \). Which of the following expressions is equal to the object’s position at time \( t = \dfrac{T}{8} \)?
On a harsh winter day, a \( 1500 \) \( \text{kg} \) vehicle takes a circular banked exit ramp (radius \( R = 150 \) \( \text{m} \); banking angle of \( 10^\circ \)) at a speed of \( 30 \) \( \text{mph} \), since the speed limit is \( 35 \) \( \text{mph} \). However, the exit ramp is completely iced up (frictionless). To make matters worse, a wind is blowing parallel to the ramp in a downward direction. The wind exerts a force of \( 3000 \) \( \text{N} \). Under these conditions, can the driver continue to follow a safe horizontal circle on the exit ramp and stay below the speed limit?
To convert \( \text{mph} \) into \( \text{m/s} \), use \( 1 \) \( \text{mi} = 1607 \) \( \text{m} \) and \( 1 \) \( \text{hr} = 3600 \) \( \text{s} \).
Two students start \( 100 \) \( \text{m} \) apart.
• Student A walks to the right at \( 2 \) \( \text{m/s} \).
• Student B walks to the left at \( 3 \) \( \text{m/s} \).
At what time do the students meet, and how far has each student walked when they collide?
A stone hangs by a fine thread from the ceiling, and a section of the same thread dangles from the bottom of the stone. If a person gives a sharp pull on the dangling thread, where is the thread likely to break: below the stone or above it? What if the person gives a slow and steady pull?
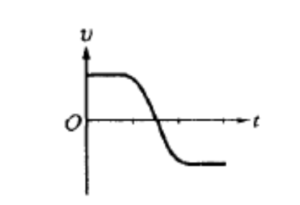
The graph above shows velocity \( v \) versus time \( t \) for an object in linear motion. Which of the following is a possible graph of position (\( x \)) versus time (\( t \)) for this object?
By continuing you (1) agree to our Terms of Use and Terms of Sale and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
Here’s guide to using 5 UBQ filters.
GQ = general question, MCQ = multiple choice, FRQ = free response.
Click the check or bookmark button.
Now you’ll be able to see completed or bookmarked questions at a glance!
Answer keys, personalized for you.
Phy will be responsible for grading your FRQs and GQs.
No more copy and pasting. Just solve and snap.
Questions for Mastery
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.
