Use this guide to estimate your score on the 2025 AP Physics 1 FRQ. It includes answer keys and projected point breakdowns (based on past rubrics). Click the headings below to open each PDF question.
Use this calculator to input your points for each FRQ and get your AP Physics 1 score.
Question 1: Momentum and Collisions (10 points total)
A. i. Momentum graph (2 points)
- (1 pt) Correct overall shape: Horizontal line through \(t_1\) and \(t_2\), making sure the line extends trough \(t_2\)
- (1 pt) Labels on the vertical axis: \( m_c v_c \)
A. ii. Expression for final speed (3 points)
- (1 pt) Implicitly or explicitly using conservation of momentum
- (1 pt) For a correct expression involving final and initial momentum of the system:
\[m_c v_c = (m_c + m_b) v_f \] - (1 pt) For a correct and final derivation for \( v_f \):
\[ v_f = \frac{m_c v_c}{m_c + m_b} = \frac{v_c}{1 + 1/5} = \mathbf{\frac{5v_c}{6}}\]
A. iii. Change in kinetic energy (3 points)
- (1 pt) Implicitly or explicitly using conservation of energy.
- Correctly states initial and final kinetic energy expressions:
\[ \Delta K = \frac{1}{2} m_c v_c^2 \,-\, \frac{1}{2} (m_c + m_b) v_f^2\] - (1 pt) For a correct substitution of known values:
\[ m_b = \frac{1}{5} m_c, v_f = \frac{5v_c}{6} \] - (1 pt) For a correct final derivation for loss of \(KE\):
\[\Delta K = \frac{1}{2} m_c v_c^2 \left( 1 \,-\, \frac{6}{5} \cdot \frac{25}{36} \right) = \mathbf{\frac{1}{12} m_c v_c^2}\]
B. Sliding block with friction (2 points)
- (1 pt) Correct answer: Remains Constant
- (1 pt) Justification: Momentum is conserved because there are no external horizontal forces acting on the system.
Sample answer for part B:
“The total momentum of the block-cart system remains constant because friction is an internal force. There are no net external horizontal forces acting on the system, so momentum is conserved even though the block slows relative to the cart.”
Question 2: Energy Conservation with Spring (12 points total)
A. Energy bar charts (3 points)
- (1 pt) At \( x = 0 \): \( U_g = 12E_0 \), \( K = 0 \), \( U_s = 0 \)
- (1 pt) At \( x = 6D \): \( U_g = 6E_0 \), \( K = 6E_0 \), \( U_s = 0 \)
- (1 pt) Bars consistent with total energy remaining constant at \( 12E_0 \)
B. Deriving spring constant (3 points)
- (1 pt) Implicitly or explicitly using conservation of energy.
\[ E_{top} = E_{bottom}\] - (1 pt) For a correctly substitution of height, or some use of \(sin\theta\)
\[ m g (12D \sin\theta) = \frac{1}{2} k (4D)^2\] - (1 pt) For a final and correctly simplified expression for \(k\)
\[ k = \frac{24mgD \sin\theta}{16D^2} = = \frac{3mg \sin\theta}{2D}\]
C. Energy vs position graph (3 points)
- (1 pt) Total energy = flat line at \( 12E_0 \)
- (1 pt) \( U_g \): a decreasing line starting from \(4E_0\) on the y-axis to \(0E_0\) on at a distance of \12D\)
D. Comparing speeds (4 points)
- (1 pt) Correct answer: \( v_9 > v_8 \)
- (1 pt) Justification including the use of conservation of energy and showing the total amount of energy \(12E_0\) is equal to the sum of \(U_g\), \(U_s\), and \(KE\).
- (1 pt) Justification including a reference to the graph: Larger vertical gap between total mechanical energy line and potential energy curve at \( x = 9D \) indicates greater kinetic energy.
- (1pt) For a clear and coherent paragraph justifying why the velocities may be differ at the given points.
Sample answer for part D:
“Since there are no external forces, energy is conserved. So to find maximum velocity (and thus maximum kinetic energy), we must minimize the sum of \(U_g\) and \(U_s\) at any given point. On the graph the kinetic energy is represented by the vertical distance between the total energy line and the combined potential (gravitational + spring) energy. Since this gap is larger at \( x = 9D \), the object has more kinetic energy and thus a greater speed.”
Question 3: Torque and Linear Graphing (10 points total)
A. Experimental setup (2 points)
- (1 pt) For a correct produce involving: hanging the masses at varying distances from the pivot, keeping the beam horizontal.
- (1 pt) For a brief explanation on how to reduce experimental uncertainty.
Sample Answer:
“Position the block at known distances from the pivot and measure the corresponding force using a spring scale. Ensure the beam is horizontal to avoid additional torques. Repeat procedure but vary the distance the mass hangs from the pivot point.”
B. Graph and analysis (2 points)
- (1 pt) Graph torque vs distance or force vs distance
- (1 pt) Use slope of line to solve for mass using \( \tau = mgr \)
Sample Answer:
“Plotting torque vs distance, the slope equals \( mg \), so we can find the mass using \( m = \text{slope} / g \).”
C. i. Vertical axis quantity (1 point)
- Correct answer: \( F_T \) or any properly rearranged variation of \(F_T\) and constants
C. ii. Graph and labels (2 points)
- (1 pt) Axes labeled \( F_T \) and \( 1/\sin\theta \)
- (1 pt) Graph with plotted data from Table 2 (data table of student calculated values)
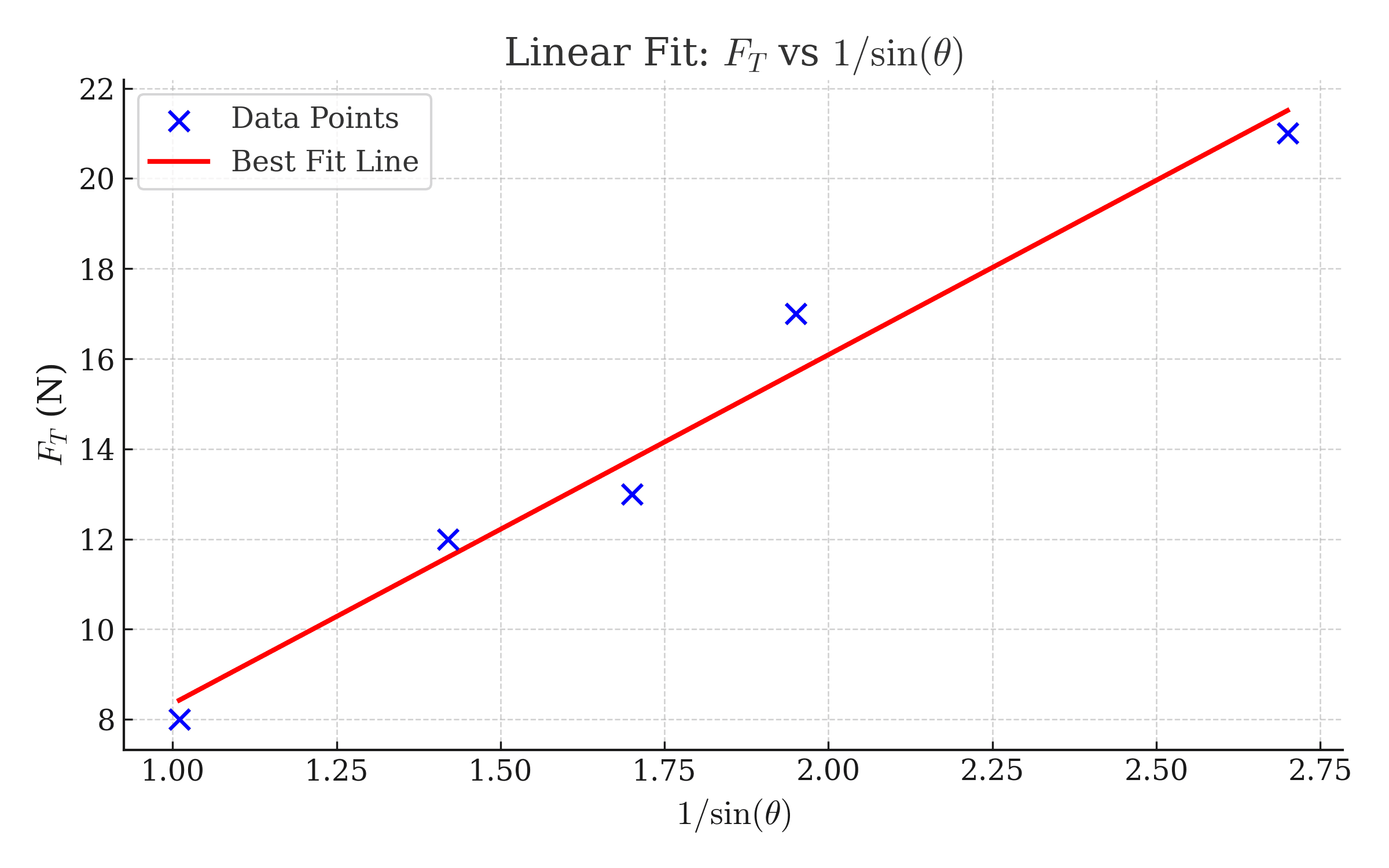
C. iii. Best-fit line (1 point)
- (1 pt) Line fits most data with reasonable accuracy
D. Calculate mass (2 points)
- (1 pt) For a correct method of finding slope using two point on the line of best fit
(1 pt) For appropriately plugging in the slope into the given equation to find mass:
\[ \text{slope} = \frac{5Mg}{6} \Rightarrow M = \frac{6 \cdot \text{slope}}{5g}\]
Sample Answer:
“Calculating the slope of the best-fit line gives us \(\approx 8\) Newtons. We can plug this into \( M = \frac{6 \cdot \text{slope}}{5g} \) which gives us a final mass value of \( M \approx 0.97 \, \text{kg} \).”
Question 4: Buoyancy and Acceleration (8 points total)
A. Compare accelerations (3 points)
- (1 pt) Correct answer: \( a_2 > a_1 \)
- (1 pt) Justification: Saltwater is denser, so buoyant force is greater.
- (1 pt) Justification: Greater buoyant force means more net upwards force, thus more acceleration.
Sample Answer:
“Saltwater has a greater density than freshwater, resulting in a larger buoyant force and a greater net upward force. This causes a higher acceleration in saltwater.”
B. Derive expression for acceleration (3 points)
- (1 pt) For explicitly or simplicity using Newton’s Second Law:
\[F_{net} = ma \] - For a correct expression for net force acting on the block
\[ F_{\text{net}} = F_b – mg = \rho Vg – mg = ma\] - (1 pt) For a complete and correct final derivation of \(a\)
\[ a = \frac{g(\rho V – m)}{m}\]
C. Consistency check (2 points)
- (1 pt) States the expression is consistent with result
- (1 pt) Justification: Greater fluid density increases acceleration
Sample Answer:
“The formula shows \( a \propto \rho \), so higher fluid density leads to greater acceleration, which agrees with the earlier conclusion that \( a_2 > a_1 \).”
Total Possible Points: 40
Please note: this is a prediction of point allocations. Official exam solution and points are expected to be released ~July, 2025. In the meantime you can input your predicted points into this calculator to see your final AP score.


