The net gravitational force on the 2.0 kg sphere will be the vector sum of the forces exerted by the 4.0 kg and 7.0 kg spheres. Since the 2.0 kg sphere is midway, each force will act along the line connecting the centers of the spheres. See the FBD below.
| Step | Formula Derivation | Reasoning |
|---|---|---|
| 1 | r_{\text{half}} = \frac{1.2 , \text{m}}{2} = 0.6 , \text{m} | Half the distance between the two spheres. |
| 2 | F_{\text{4 to 2}} = G \frac{4 \times 2}{0.6^2} | Gravitational force between the 4.0 kg and 2.0 kg spheres. |
| 3 | F_{\text{7 to 2}} = G \frac{7 \times 2}{0.6^2} | Gravitational force between the 7.0 kg and 2.0 kg spheres. |
| 4 | F_{\text{net}} = F_{\text{7 to 2}} – F_{\text{4 to 2}} | Net force is the difference between the two forces, as they are in opposite directions. |
Let’s calculate the net gravitational force.
| Step | Formula Derivation | Reasoning |
|---|---|---|
| 4 | F_{\text{net}} \approx 1.11 \times 10^{-9} , \text{N} | Calculated net gravitational force. |
The net gravitational force on the 2.0 kg sphere, located midway between the 4.0 kg and 7.0 kg spheres (1.2 m apart), is approximately \boxed{1.11 \times 10^{-9} , \text{Newtons}} . This force is directed towards the 7.0 kg sphere due to its larger mass.
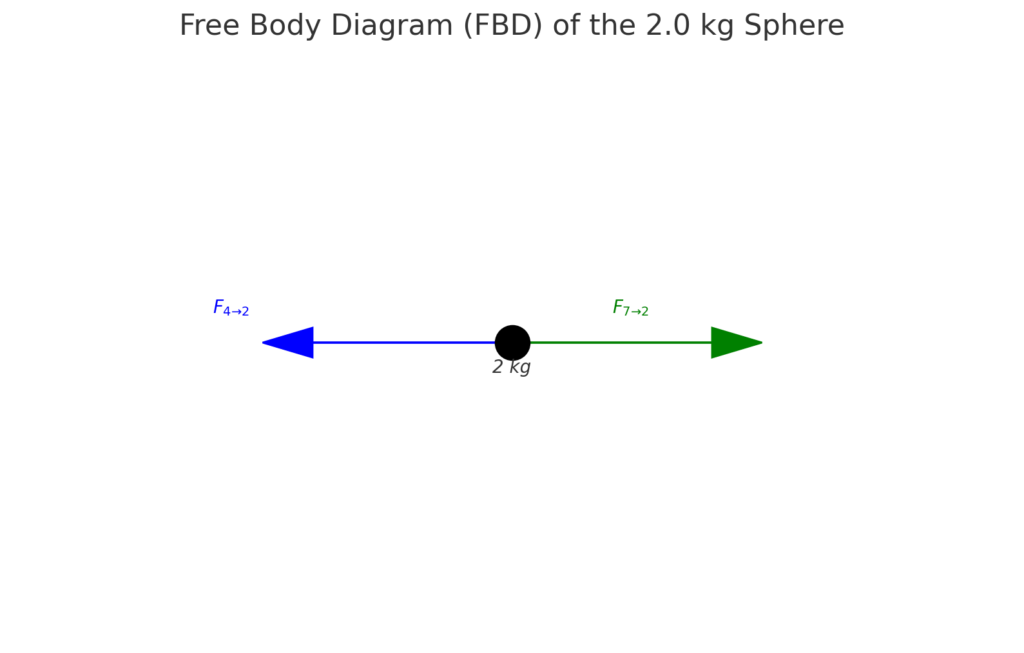
These forces indicate the gravitational pull exerted on the 2.0 kg sphere from each of the other two spheres. In this scenario, the net force is the vector sum of these two forces, with the direction towards the 7.0 kg sphere due to its larger mass.
Phy can also check your working. Just snap a picture!
While traveling in its elliptical orbit around the Sun, Mars gains speed during the part of the orbit where it is getting closer to the Sun. Which of the following can be used to explain this gain in speed?
A 1.5 kg object is located at a distance of 1.7 x106 m from the center of a larger object whose mass is 7.4 x 1022 kg.
A satellite in circular orbit around the Earth moves at constant speed. This orbit is maintained by the force of gravity between the Earth and the satellite, yet no work is done on the satellite. How is this possible?
A child on Earth has a weight of 500N. Determine the weight of the child if the earth was to triple in both mass and radius (3M and 3r).
Two identical satellites are placed in orbit of two different planets. Satellite A orbits Mars, and Satellite B orbits Jupiter. The orbital speeds of each satellite are the same. Which satellite has a greater orbital radius?
Fnet = 1.11 x 10-9
By continuing you (1) agree to our Terms of Sale and Terms of Use and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
| Kinematics | Forces |
|---|---|
| \Delta x = v_i t + \frac{1}{2} at^2 | F = ma |
| v = v_i + at | F_g = \frac{G m_1m_2}{r^2} |
| a = \frac{\Delta v}{\Delta t} | f = \mu N |
| R = \frac{v_i^2 \sin(2\theta)}{g} |
| Circular Motion | Energy |
|---|---|
| F_c = \frac{mv^2}{r} | KE = \frac{1}{2} mv^2 |
| a_c = \frac{v^2}{r} | PE = mgh |
| KE_i + PE_i = KE_f + PE_f |
| Momentum | Torque and Rotations |
|---|---|
| p = m v | \tau = r \cdot F \cdot \sin(\theta) |
| J = \Delta p | I = \sum mr^2 |
| p_i = p_f | L = I \cdot \omega |
| Simple Harmonic Motion |
|---|
| F = -k x |
| T = 2\pi \sqrt{\frac{l}{g}} |
| T = 2\pi \sqrt{\frac{m}{k}} |
| Constant | Description |
|---|---|
| g | Acceleration due to gravity, typically 9.8 , \text{m/s}^2 on Earth’s surface |
| G | Universal Gravitational Constant, 6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2 |
| \mu_k and \mu_s | Coefficients of kinetic (\mu_k) and static (\mu_s) friction, dimensionless. Static friction (\mu_s) is usually greater than kinetic friction (\mu_k) as it resists the start of motion. |
| k | Spring constant, in \text{N/m} |
| M_E = 5.972 \times 10^{24} , \text{kg} | Mass of the Earth |
| M_M = 7.348 \times 10^{22} , \text{kg} | Mass of the Moon |
| M_M = 1.989 \times 10^{30} , \text{kg} | Mass of the Sun |
| Variable | SI Unit |
|---|---|
| s (Displacement) | \text{meters (m)} |
| v (Velocity) | \text{meters per second (m/s)} |
| a (Acceleration) | \text{meters per second squared (m/s}^2\text{)} |
| t (Time) | \text{seconds (s)} |
| m (Mass) | \text{kilograms (kg)} |
| Variable | Derived SI Unit |
|---|---|
| F (Force) | \text{newtons (N)} |
| E, PE, KE (Energy, Potential Energy, Kinetic Energy) | \text{joules (J)} |
| P (Power) | \text{watts (W)} |
| p (Momentum) | \text{kilogram meters per second (kgm/s)} |
| \omega (Angular Velocity) | \text{radians per second (rad/s)} |
| \tau (Torque) | \text{newton meters (Nm)} |
| I (Moment of Inertia) | \text{kilogram meter squared (kgm}^2\text{)} |
| f (Frequency) | \text{hertz (Hz)} |
General Metric Conversion Chart
Example of using unit analysis: Convert 5 kilometers to millimeters.
Start with the given measurement: \text{5 km}
Use the conversion factors for kilometers to meters and meters to millimeters: \text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}}
Perform the multiplication: \text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}} = 5 \times 10^3 \times 10^3 \, \text{mm}
Simplify to get the final answer: \boxed{5 \times 10^6 \, \text{mm}}
Prefix | Symbol | Power of Ten | Equivalent |
|---|---|---|---|
Pico- | p | 10^{-12} | 0.000000000001 |
Nano- | n | 10^{-9} | 0.000000001 |
Micro- | µ | 10^{-6} | 0.000001 |
Milli- | m | 10^{-3} | 0.001 |
Centi- | c | 10^{-2} | 0.01 |
Deci- | d | 10^{-1} | 0.1 |
(Base unit) | – | 10^{0} | 1 |
Deca- or Deka- | da | 10^{1} | 10 |
Hecto- | h | 10^{2} | 100 |
Kilo- | k | 10^{3} | 1,000 |
Mega- | M | 10^{6} | 1,000,000 |
Giga- | G | 10^{9} | 1,000,000,000 |
Tera- | T | 10^{12} | 1,000,000,000,000 |
The most advanced version of Phy. Currently 50% off, for early supporters.
per month
Billed Monthly. Cancel Anytime.
Trial –> Phy Pro
A quick explanation
UBQ credits are specifically used to grade your FRQs and GQs.
You can still view questions and see answers without credits.
Submitting an answer counts as 1 attempt.
Seeing answer or explanation counts as a failed attempt.
Lastly, check your average score, across every attempt, in the top left.
MCQs are 1 point each. GQs are 1 point. FRQs will state points for each part.
Phy can give partial credit for GQs & FRQs.
Phy sees everything.
It customizes responses, explanations, and feedback based on what you struggle with. Try your best on every question!
Understand you mistakes quicker.
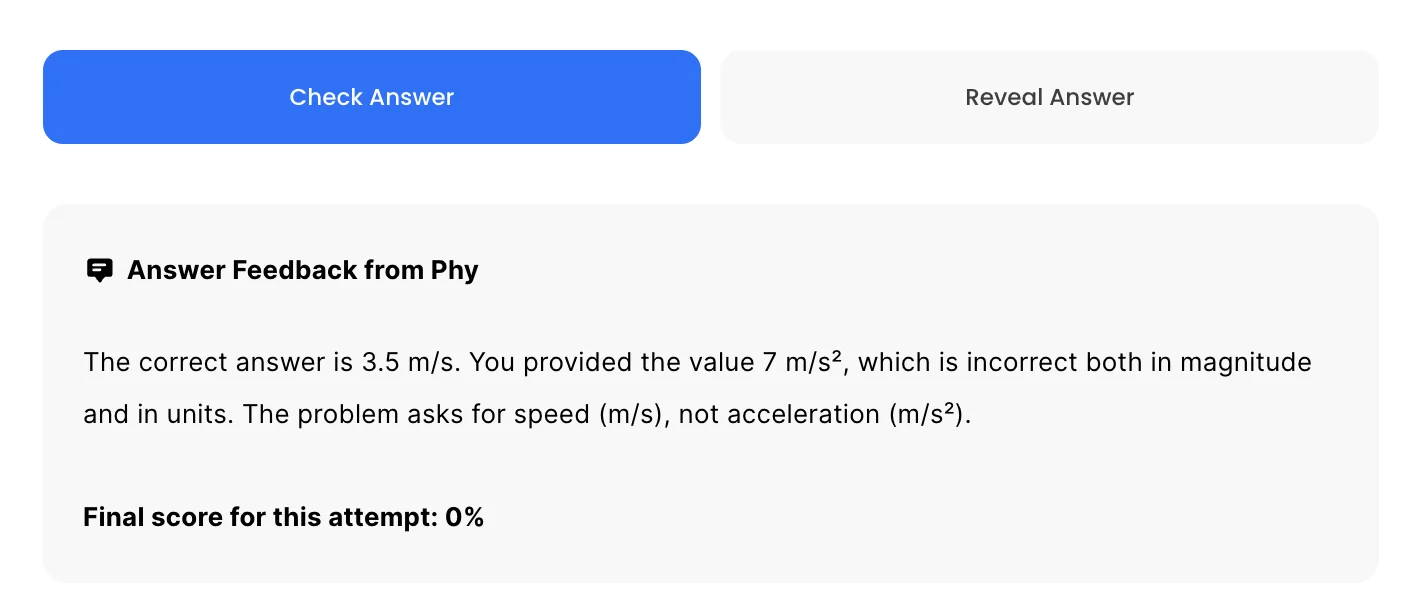
For GQs and FRQs, Phy provides brief feedback as to how you can improve your answer.
Aim to increase your understadning and average score with every attempt!
10 Free Credits To Get You Started
*Phy Pro members get unlimited credits
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.