# Part A: Calculate velocity of the bullet + wooden block just after impact
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | m_1 = 0.0500 \, \text{kg} | Mass of the bullet. |
| 2 | u_1 = 50.0 \, \text{m/s} | Initial velocity of the bullet. |
| 3 | m_2 = 0.300 \, \text{kg} | Mass of the wooden block. |
| 4 | u_2 = 0 \, \text{m/s} | Initial velocity of the wooden block (at rest). |
| 5 | v = \frac{m_1 u_1 + m_2 u_2}{m_1 + m_2} | Formula for the final velocity after a completely inelastic collision, where m_1 and m_2 are masses of the bullet and block, u_1 and u_2 are their initial velocities respectively. |
| 6 | v = \frac{(0.0500 \, \text{kg}) (50.0 \, \text{m/s}) + (0.300 \, \text{kg}) (0 \, \text{m/s})}{0.0500 \, \text{kg} + 0.300 \, \text{kg}} | Substitute the values of m_1 , m_2 , u_1 , and u_2 into the formula. |
| 7 | \mathbf{v = 7.14 \, \text{m/s}} | Compute to find the final velocity of the bullet + wooden block system just after the collision. |
# Part B: Calculate the vertical distance h reached by the bullet and wooden block
| Step | Derivation/Formula | Reasoning |
|---|---|---|
| 1 | v = 7.14 \, \text{m/s} | Initial velocity of the system after impact (from part A). |
| 2 | v^2 = u^2 + 2gh | Use the kinematic equation relating initial velocity (u), final velocity (v), acceleration due to gravity (g), and height (h). Since the system comes to a stop at the highest point, final velocity v is 0. |
| 3 | 0 = (7.14 \, \text{m/s})^2 + 2(-9.81 \, \text{m/s}^2)h | At the highest point the final velocity is 0, and acceleration due to gravity (a negative value, since it acts downwards) impacts the rising object. |
| 4 | h = \frac{(7.14 \, \text{m/s})^2}{2 \times 9.81 \, \text{m/s}^2} | Rearrange to solve for h. |
| 5 | \mathbf{h = 2.59 \, \text{m}} | Compute the vertical height. |
# Part C: Compare effects of doubling the bullet’s mass vs. velocity on h
| Comparison | Analysis | Conclusion |
|---|---|---|
| Doubling bullet’s velocity | h_f \propto v^2 , doubling v would quadruple h (since h_f = \frac{4v^2}{2g} ) | Increase in velocity has a significant effect, leading to an increase by a factor of four for h . |
| Doubling bullet’s mass | h_f determined more by v (system velocity) than by mass directly. Increasing mass lowers system velocity, hence slightly lowering h . | Little to no increase in h ; could actually decrease due to lower velocity after collision. |
| None | Analysis shows that velocity change impacts height significantly compared to mass change. | (ii) Doubling the bullet’s velocity has a greater effect on height than doubling the bullet’s mass. |
Phy can also check your working. Just snap a picture!
One end of a spring is attached to a solid wall while the other end just reaches to the edge of a horizontal, frictionless tabletop, which is a distance h above the floor. A block of mass M is placed against the end of the spring and pushed toward the wall until the spring has been compressed a distance x . The block is released and strikes the floor a horizontal distance D from the edge of the table. Air resistance is negligible.
Derive an expressions for the following quantities only in terms of M, x, D, h, and any constants.
If a small motor does 520 J of work to move a toy car 260 meters in a time of 37 seconds.
While traveling in its elliptical orbit around the Sun, Mars gains speed during the part of the orbit where it is getting closer to the Sun. Which of the following can be used to explain this gain in speed?
A vehicle is moving at a speed of 12.3 m/s on a decline when the brakes of all four wheels are fully applied, causing them to lock. The slope of the decline forms an angle of 18.0 degrees with the horizontal plane. Given that the coefficient of kinetic friction between the tires and the road surface is 0.650.
In which one of the following circumstances does the principle of conservation of mechanical energy apply, even though a nonconservative force acts on the moving object?
(a) 7.1 m/s
(b) 2.6 m
(c) ii
By continuing you (1) agree to our Terms of Sale and Terms of Use and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
| Kinematics | Forces |
|---|---|
| \Delta x = v_i t + \frac{1}{2} at^2 | F = ma |
| v = v_i + at | F_g = \frac{G m_1m_2}{r^2} |
| a = \frac{\Delta v}{\Delta t} | f = \mu N |
| R = \frac{v_i^2 \sin(2\theta)}{g} |
| Circular Motion | Energy |
|---|---|
| F_c = \frac{mv^2}{r} | KE = \frac{1}{2} mv^2 |
| a_c = \frac{v^2}{r} | PE = mgh |
| KE_i + PE_i = KE_f + PE_f |
| Momentum | Torque and Rotations |
|---|---|
| p = m v | \tau = r \cdot F \cdot \sin(\theta) |
| J = \Delta p | I = \sum mr^2 |
| p_i = p_f | L = I \cdot \omega |
| Simple Harmonic Motion |
|---|
| F = -k x |
| T = 2\pi \sqrt{\frac{l}{g}} |
| T = 2\pi \sqrt{\frac{m}{k}} |
| Constant | Description |
|---|---|
| g | Acceleration due to gravity, typically 9.8 , \text{m/s}^2 on Earth’s surface |
| G | Universal Gravitational Constant, 6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2 |
| \mu_k and \mu_s | Coefficients of kinetic (\mu_k) and static (\mu_s) friction, dimensionless. Static friction (\mu_s) is usually greater than kinetic friction (\mu_k) as it resists the start of motion. |
| k | Spring constant, in \text{N/m} |
| M_E = 5.972 \times 10^{24} , \text{kg} | Mass of the Earth |
| M_M = 7.348 \times 10^{22} , \text{kg} | Mass of the Moon |
| M_M = 1.989 \times 10^{30} , \text{kg} | Mass of the Sun |
| Variable | SI Unit |
|---|---|
| s (Displacement) | \text{meters (m)} |
| v (Velocity) | \text{meters per second (m/s)} |
| a (Acceleration) | \text{meters per second squared (m/s}^2\text{)} |
| t (Time) | \text{seconds (s)} |
| m (Mass) | \text{kilograms (kg)} |
| Variable | Derived SI Unit |
|---|---|
| F (Force) | \text{newtons (N)} |
| E, PE, KE (Energy, Potential Energy, Kinetic Energy) | \text{joules (J)} |
| P (Power) | \text{watts (W)} |
| p (Momentum) | \text{kilogram meters per second (kgm/s)} |
| \omega (Angular Velocity) | \text{radians per second (rad/s)} |
| \tau (Torque) | \text{newton meters (Nm)} |
| I (Moment of Inertia) | \text{kilogram meter squared (kgm}^2\text{)} |
| f (Frequency) | \text{hertz (Hz)} |
General Metric Conversion Chart
Example of using unit analysis: Convert 5 kilometers to millimeters.
Start with the given measurement: \text{5 km}
Use the conversion factors for kilometers to meters and meters to millimeters: \text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}}
Perform the multiplication: \text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}} = 5 \times 10^3 \times 10^3 \, \text{mm}
Simplify to get the final answer: \boxed{5 \times 10^6 \, \text{mm}}
Prefix | Symbol | Power of Ten | Equivalent |
|---|---|---|---|
Pico- | p | 10^{-12} | 0.000000000001 |
Nano- | n | 10^{-9} | 0.000000001 |
Micro- | µ | 10^{-6} | 0.000001 |
Milli- | m | 10^{-3} | 0.001 |
Centi- | c | 10^{-2} | 0.01 |
Deci- | d | 10^{-1} | 0.1 |
(Base unit) | – | 10^{0} | 1 |
Deca- or Deka- | da | 10^{1} | 10 |
Hecto- | h | 10^{2} | 100 |
Kilo- | k | 10^{3} | 1,000 |
Mega- | M | 10^{6} | 1,000,000 |
Giga- | G | 10^{9} | 1,000,000,000 |
Tera- | T | 10^{12} | 1,000,000,000,000 |
The most advanced version of Phy. Currently 50% off, for early supporters.
per month
Billed Monthly. Cancel Anytime.
Trial –> Phy Pro
A quick explanation
UBQ credits are specifically used to grade your FRQs and GQs.
You can still view questions and see answers without credits.
Submitting an answer counts as 1 attempt.
Seeing answer or explanation counts as a failed attempt.
Lastly, check your average score, across every attempt, in the top left.
MCQs are 1 point each. GQs are 1 point. FRQs will state points for each part.
Phy can give partial credit for GQs & FRQs.
Phy sees everything.
It customizes responses, explanations, and feedback based on what you struggle with. Try your best on every question!
Understand you mistakes quicker.
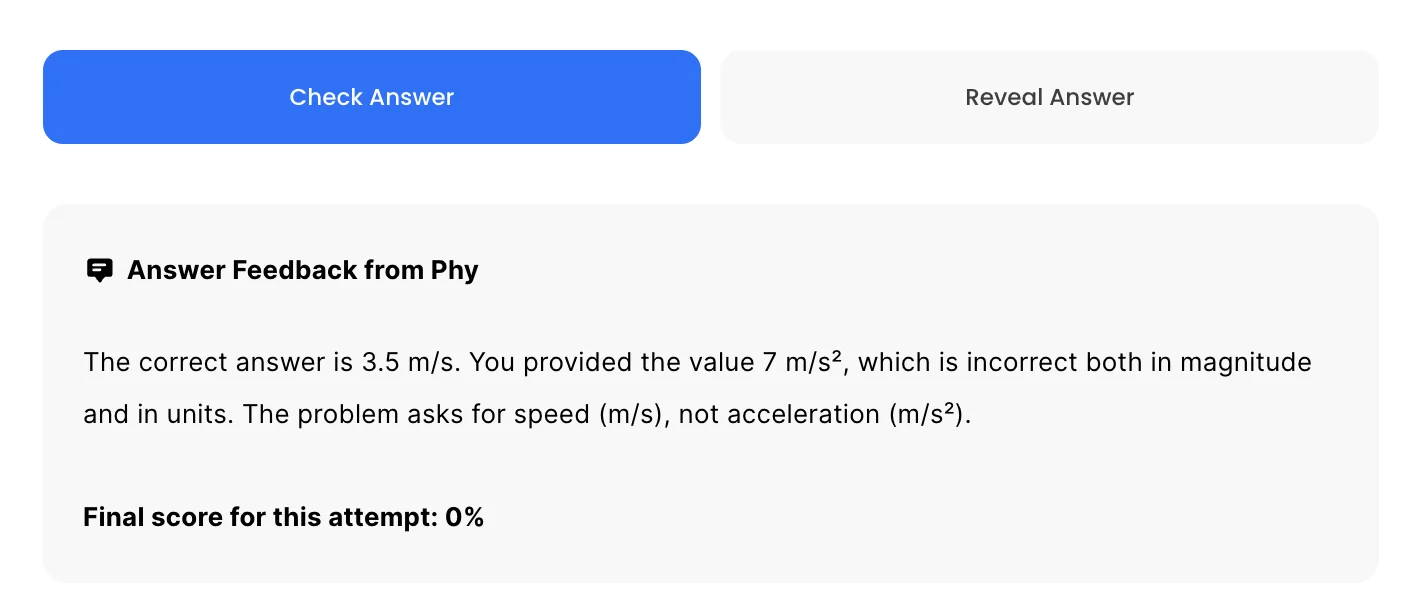
For GQs and FRQs, Phy provides brief feedback as to how you can improve your answer.
Aim to increase your understadning and average score with every attempt!
10 Free Credits To Get You Started
*Phy Pro members get unlimited credits
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.