for free to use all UBQ features
A block with a mass of \( 4 \) \( \text{kg} \) is attached to a spring on the wall that oscillates back and forth with a frequency of \( 4 \) \( \text{Hz} \) and an amplitude of \( 3 \) \( \text{m} \). What would the frequency be if the block were replaced by one with one‑fourth the mass and the amplitude of the block is increased to \( 9 \) \( \text{m} \)?
Which statements are not valid for a projectile? Take up as positive.
A rollercoaster leaves the station at rest. Its speed increases steadily for \( 6 \) \( \text{s} \) as it heads down the first drop. The ride then levels out and it moves at a constant speed for \( 4 \) \( \text{s} \) before hitting the brakes and stopping in \( 3 \) \( \text{s} \). Draw the velocity vs. time graph or explain it in terms of functions.
You are lying in bed and want to shut your bedroom door. You have a bouncy “superball” and a blob of clay, both with the same mass \( m \). Which one would be more effective to throw at your door to close it?
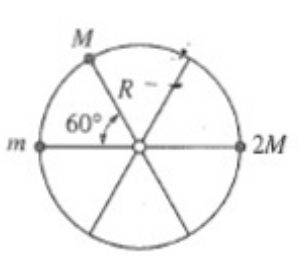
A wheel of radius \( R \) and negligible mass is mounted on a horizontal frictionless axle so that the wheel is in a vertical plane. Three small objects having masses \( m \), \( M \), and \( 2M \), respectively, are mounted on the rim of the wheel, as shown above. If the system is in static equilibrium, what is the value of \( m \) in terms of \( M \)?
To increase the moment of inertia of a body about an axis, you must
An \( 80 \, \text{kg} \) block is placed \( 2 \, \text{m} \) away from the endpoint of a horizontal steel beam of length \( 6.6 \, \text{m} \) and mass \( 1,450 \, \text{kg} \). The plank makes contact with a vertical wall on one end (assume it does not slip). The other end of the beam is attached to a massless cable that makes an angle of \( 30^\circ \) with the horizontal and ties into the vertical wall as well. Calculate the (1) tension force in the cable and (2) the total force the wall exerts on the beam.
Wanda watches the fish in her fish tank and notices that the angelfish like to feed at the water’s surface, while the catfish feed \( 0.300 \) \( \text{m} \) below at the bottom of the tank. If the average density of the water in the tank is \( 1000\) \( \text{kg/m}^3 \), what is the absolute pressure on the catfish?
A car starts from rest and accelerates uniformly over a time of 5 seconds for a distance of 100 m. Determine the acceleration of the car.
A Christmas ornament made from a thin hollow glass sphere hangs from a thin wire of negligible mass. It is observed to oscillates with a frequency of \( 2.50 \) \( \text{Hz} \) in a city where \( g = 9.80 \) \( \text{m/s}^2 \). What is the radius of the ornament? The moment of inertia of the ornament is given by \( I = \frac{5}{3} mr^2 \).
You kick a ball straight up. Compare the sign of the work done by gravity on the ball while it goes up with the sign of the work done by gravity while it goes down.
What is the weight of a person who has a mass of \(75 \, \text{kg}\)?
Which launch angle gives the greatest horizontal range, assuming level ground and no air resistance?
Which graph below shows that one of the runners started 10 meters further ahead of the other? Assume the y-axis is measured in meters and the x-axis is measured in seconds.
A \(0.5 \, \text{kg}\) cart, on a frictionless \(2 \, \text{m}\) long table, is being pulled by a \(0.1 \, \text{kg}\) mass connected by a string and hanging over a pulley. The system is released from rest. After the hanging mass falls \(0.5 \, \text{m}\), calculate the speed of the cart on the table. Use ONLY forces and energy.
Two workers are holding a thin plate with length \(5 \, \text{m}\) and height \(2 \, \text{m}\) at rest by supporting the plate in the bottom corners. The workers are standing at rest on a slope of \(10^\circ\). Treat these supporting forces as vertical normal forces and calculate their magnitudes and state if both workers are sharing “the job” fairly.

A simple pendulum consists of a bob of mass 1.8 kg attached to a string of length 2.3 m. The pendulum is held at an angle of 30° from the vertical by a light horizontal string attached to a wall, as shown above.
Two blocks of ice, one five times as heavy as the other, are at rest on a frozen lake. A person then pushes each block the same distance \(d\). Ignore friction and assume that an equal force \(F\) is exerted on each block. Which of the following statements is true about the kinetic energy of the heavier block after the push?
A toy car moves off the edge of a table that is \(1.25 \, \text{m}\) high. If the car lands \(0.40 \,\text{m}\) from the base of the table…
A tennis ball is thrown straight up with an initial speed of \( 22.5 \, \text{m/s} \). It is caught at the same distance above ground.
Two identical satellites are placed in orbit of two different planets. Satellite \(A\) orbits Mars, and Satellite \(B\) orbits Jupiter. The orbital speeds of each satellite are the same. Which satellite has a greater orbital radius?
A car travels at \( 20 \, \text{m/s} \) for \( 5 \, \text{mins} \) and then travels another \( 2 \, \text{km} \) at \( 40 \, \text{m/s} \). What is the total distance traveled and time of travel for the car?
Divers in Acapulco jump from a cliff that is \( 36 \, \text{m} \) above the water with an initial vertical velocity of \( 2 \, \text{m/s} \).
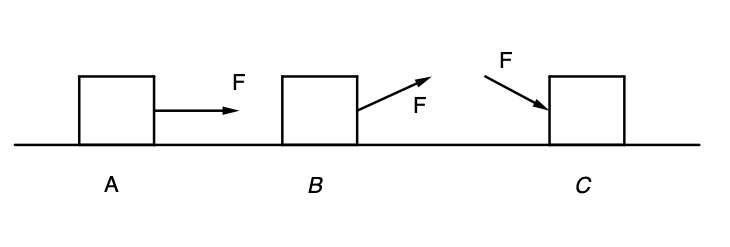
Three identical blocks are being pulled or pushed across a rough horizontal surface by force of identical magnitude F, as shown in the drawing below. Rank the kinetic frictional forces that act on the blocks from smallest to greatest.
By continuing you (1) agree to our Terms of Use and Terms of Sale and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
Quick Start Guide
AP physics 1, AP C, honors and advanced physics students.
Quickly filter questions by units and more.


Here’s guide to using 5 UBQ filters.
GQ = general question, MCQ = multiple choice, FRQ = free response.

Click the check or bookmark button.
Now you’ll be able to see completed or bookmarked questions at a glance!
Answer keys, personalized for you.
Phy will be responsible for grading your FRQs and GQs.
No more copy and pasting. Just solve and snap.
Questions for Mastery
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.