This course article contains videos that can only be accessed once enrolled in the Learn AP Physics from Scratch Course.
Unit 2 Breakdown
You are on Lesson 3 of 8:
- Unit 2.1 | Understanding and Applying Newton’s Law in Depth
- Unit 2.2 | Common Linear Forces, Equations, and Misconceptions
- Unit 2.3 | Drawing and Understanding Force Body Diagrams [Current Lesson]
- Unit 2.4 | Deriving Equations to Solve Linear Force Problems
- Unit 2.5 | Advanced Force Problems – Tension and Elevators
- Unit 2.6 | Advanced Force Problems – Ramps (Inclines)
- Unit 2.7 | Advanced Force Problems – Pulley System
- Unit 2.8 | Advanced Force Problems – Multi-Body System
In this lesson you will learn:
- What are force body diagrams (FBD)
- Steps to draw an FBD
- Direction of net force and acceleration
- Practice drawing FBDs of complex situations
- Common Misconceptions
What are FBDs?
FBD is short for “Force Body Diagram.”
It is a drawing, like the one below, showing all forces acting ON a object.
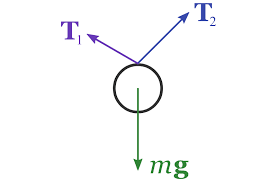
We use FBDs to visualize and simplify complex problems.
While this may seem simple, there’s a lot of important rules and concepts to apply on FBDs.
The best way to learn is to read the steps below, then do a lot of practice.
Steps for Drawing FBDs
As we go through the steps, keep the following example situation in mind. We will refer back to this and see how the rules apply: A box being pushed to the right at a constant speed across the floor.
- Draw a DOT to represent an object.
- For the situation above you would draw a small dot to represent the box.
- Identify, then draw all forces acting on the object according to the force rules (cover in 2.2)
- In this case, there is a very clear pushing force. On your dot, you would draw an arrow to the right and label it Fpush or Fapplied.
- Check for hidden forces.
- In this case the box is moving at constant speed. This means that there should be zero acceleration and zero net force. So another force is needed to cancel out Fpush. This would be the force of friction (f) acting equal but opposite to Fpush.
Let’s try some harder problems together. Be sure to read the important rules first.
5 Important Rules
- Generally all objects will have a weight force. Weight ALWAYS points straight down.
- The direction of the net force is the direction of your acceleration
- Constant speed means 0 acceleration and thus 0 net force
- Kinetic friction always acts OPPOSITE to the object’s direction of motion.
- Normal force is drawn perpendicular (90°) to the surface.
PS – FDBs
Below are some common situations you will encounter. Try drawing an FBD for these 8 problems. Then watch the short video for the explanations for each.
- A basket is suspended by a rope from the ceiling.
- A rightward force is applied to a book to accelerate it across a rough desk.
- A car applies its brakes to slow down.
- A skydiver descends with constant velocity.
- A box rests on a sloped incline.
- An elevator is traveling up and slowing down
- Five seconds after you kick a soccer ball in the air (air resistance is negligible)
- Two cables suspend a heavy neon sign at 45° angles
How many did you get right? If you got 7 or more right, you are ready to move on to the next lesson.
If you need more practice, here are some FBD worksheets: [Enroll For Material Access].
Lesson 2.3 Recap
In this lesson we covered how to quickly and accurately draw an FBD.
You got to apply your knowledge to challenging practice questions then watched me solve them.
Lesson 2.4 Preview
In the next lesson we will use FBDs to to derive equations and solve interesting, real world problems. This is generally what most students find hard in Physics. But we will break it down and make it super easy to understand.