This course article contains videos that can only be accessed once enrolled in the Learn AP Physics from Scratch Course.
Unit 2 Breakdown
You are on Lesson 4 of 8:
- Unit 2.1 | Understanding and Applying Newton’s Law in Depth
- Unit 2.2 | Common Linear Forces, Equations, and Misconceptions
- Unit 2.3 | Drawing and Understanding Force Body Diagrams
- Unit 2.4 | Deriving Equations to Solve Linear Force Problems [Current Lesson]
- Unit 2.5 | Advanced Force Problems – Tension and Elevators
- Unit 2.6 | Advanced Force Problems – Ramps (Inclines)
- Unit 2.7 | Advanced Force Problems – Pulley System
- Unit 2.8 | Advanced Force Problems – Multi-Body System
In this lesson:
- Derivation vs Memorization
- Differentiate between static and non static situations
- How to begin any problem – a framework for force problems
- Solving single-body linear force problems
Derivation vs Memorization
A HUGE misconception is that you will be given equations. This is false.
Physics, especially AP Physics 1, is all about deriving or making your own equations.
This is what makes Physics so fun! No one is given the right equation. To solve a problem you must create your own equation as you will learn in this lesson.
It’s a game of strategy, logic, and basic algebra.
Types of Force Problems
This Unit will cover problems only involving linear forces.
This includes tension, pulleys, ramps, friction, and many a few other types of problems. Sometimes it will be a combination of them.
Static vs Non-Static Systems
To help draw your FDB, you need to determine if the system is static or non-static. Here how:
| Static System | Non-Static System |
| Zero net force both x and y directions (aka: in equilibrium) | Net force in x and/or y directions (aka: not in equilibrium) |
| Not Accelerating | Accelerating in the direction of net force |
| Example: Sign hanging from two cables | Example: Pulling a box across a frictionless floor |
Single body vs Multi-body Systems
Another thing to look for in a problem is the number of masses (objects).
Most problems will only have one object. For example a box being pushed across a floor or a person moving in an elevator. These problems, static or non-static, can be solved using the framework below, which is the focus of this lesson.
Some problems, however, will have multiple objects. For example a pulley system with masses on both ends. Or two blocks stacked upon each other each. You will learn to solve in the last lesson of the Unit (2.8 – Solving Multi Body Systems)
Problem Solving Framework – Single Body Force Problems
A framework is a general procedure to tackle a specific problem. Remember that this framework will guide you to solve problems. This is NOT a substitute for logic.
- Read the problem and turn the main object into an FBD. Make sure to think about any non-obvious forces, like friction or normal forces, that maybe acting on the object
- Break apart force vectors at angles into their x and y components.
- Find the net force in the x and y direction separately. This can be done with real numbers or in terms of variables, if not given numbers.
- Use Fnet = ma! Set the net force that you found equal to ma. Rearrange and solve for the missing variable
This might be confusing. So lets apply it to a simple problem below. I’ll label the steps, so you can refer back to the framework above.
Example Problem
Problem: Using a light cord, you pull a 5kg box with a force of 20N across a rough floor. The floor has a coefficient of kinetic friction of .5 and the cord makes an angle of 30 degrees to the horizontal. What is the acceleration of the box?
Apply the framework:
- Forces acting on this box include, Tension (T), kinetic friction (fk), weight (mg), and normal force (N). Draw these forces on an FBD, like the one below.
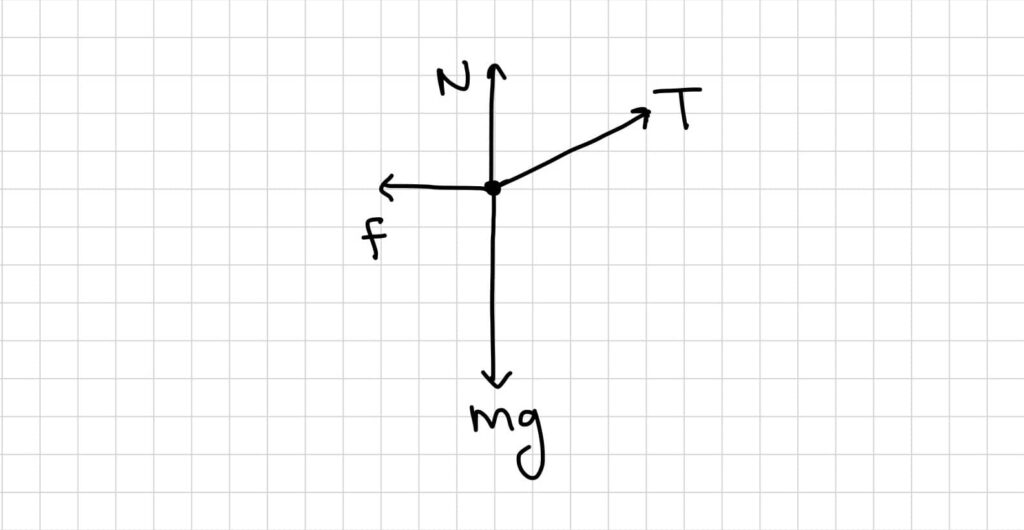
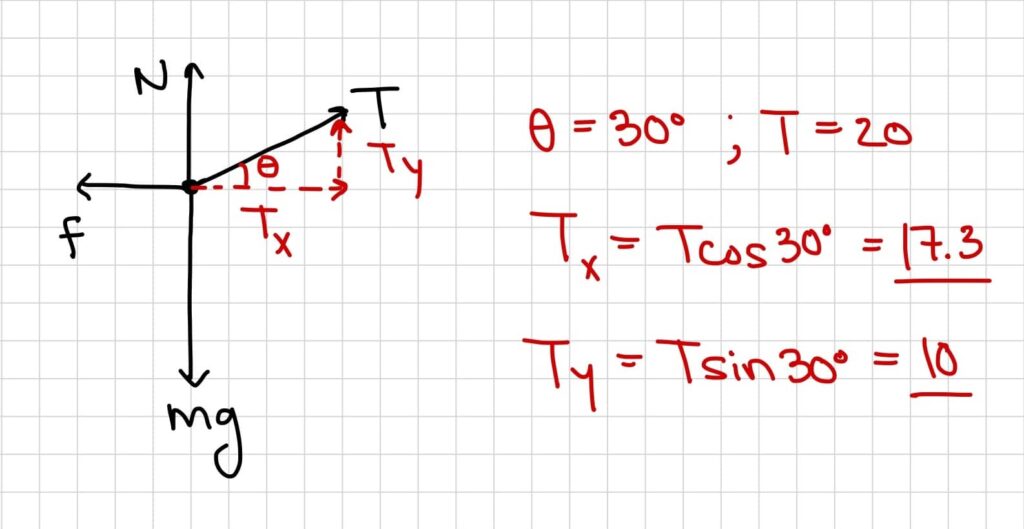
- Notice the Tension force is at a 30° angle. Break up tension in x and y components and find the value of each side. Note that you can completely solve to find a numerical value OR you can leave in terms of variables (as recommended)
- Find the Fnet(x) by adding up all the horizontal vectors in terms of the variables. Do the same for the vertical direction. Again, I would recommend doing this in terms of variables and not numbers.
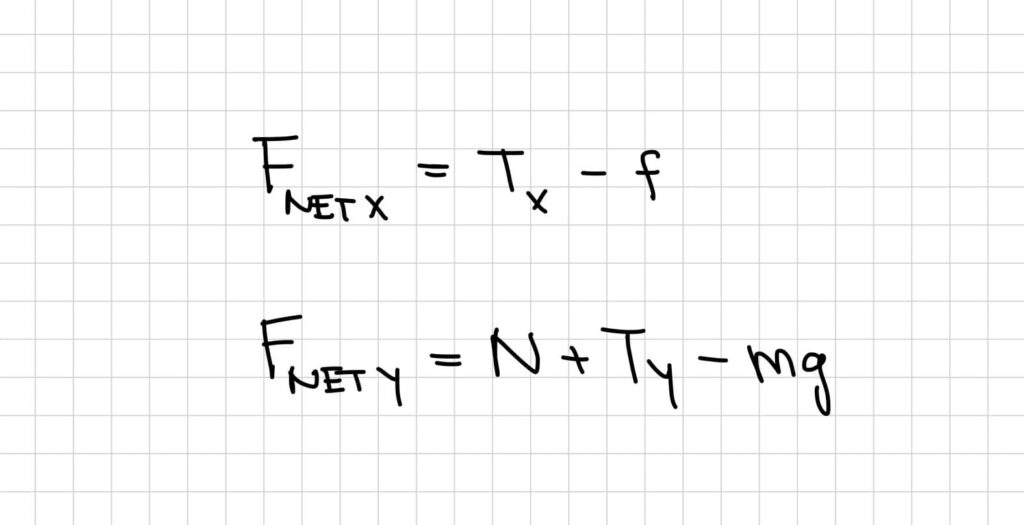
- Newton’s 2nd Law (F = ma) tell us to set first set Fnet(x) = max and then Fnet(y) = may.
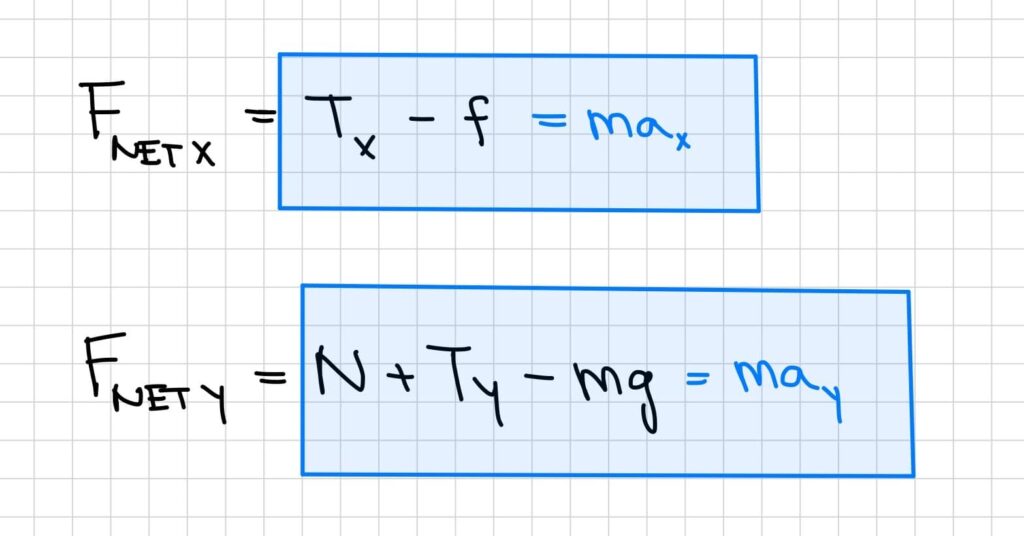
- Begin to solve the first equation Fnet(x) for ax , as this is what the problem asks us to find.
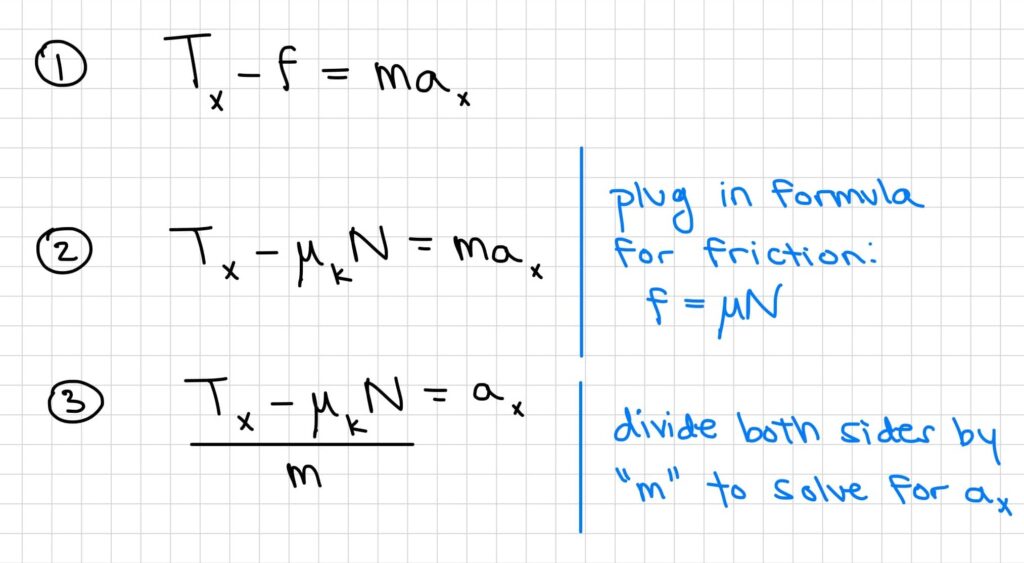
- Pause here, and notice, that we can now plug in all number EXCEPT for N (the normal force). This means we must go to our second equation (Fnet(y)) to find a value for normal force.

- Now that we have a value for normal force (39.1 N), go back to the first equation Fnet(x) and plug in all the numbers. This is written as step #4 in the image below.

LRN – Force Framework
Still having trouble understanding the force problem solving framework? Watch the short video below where I go over an example problem and apply the framework.
Practice Single Body Force Problems
All questions involve single objects that are either static or non-static. Follow the framework above to solve each problem. Over the next few lessons, you will learn to solve more complex force questions.
- Level 1: You push a 20kg box to the right with a force of 90 N across a rough floor (µk = .4). What is the box’s acceleration?
- Level 2: A large 100kg sign in suspended from two ropes that are both at an angle of 45° to the horizontal. What is the tension in each rope?
- Level 3: A 12.0 kg box is being pulled along level ground by a 81 N force that is directed at an angle of 18° above the horizontal. The coefficient of kinetic friction is 0.330. What is the acceleration of the box?
- Level 4: You pull a 10kg wagon with an constant unknown force at a 25° angle above the horizontal. The wagon accelerates at a rate of .6 m/s2. The coefficient of friction is µk= .25 between the between the tires and the road. How much force are you pulling with?
- Level 5: Conceptual – Suppose two people are pushing two identical boxes across a floor with µk = .2. Person A pushes down at an angle of 45° while Person B pushes the box upwards at an angle of 45°. Which person will move the box further after 60 seconds?
Show Answers
- 1/2 m/s2
- 707.1 N
- 3.8 m/s2
- 22.97 N
- Person A will have the greater net force, thus greater acceleration, thus furthest distance completed in 60 seconds.
PS – Single Body Linear Forces
In this video I use the force problem solving framework to solve the Level 1, 2, and 3 problems from above.
Bonus AP Level Question
A 50 kg box at rest on a rough horizontal surface. The surface has a value of µs = .75 and a µk = .3. If you pushed the box with 300 N horizontal force, how fast would the box accelerate? If you pushed the box with a horizontal force of 500 N, how fast would the box accelerate?
Show Answer
If pushed with a force of 300 N, the box would NOT accelerate (a = 0 m/s2).
If pushed with a force of 500 N, the box would overcome static friction and acclerate at a rate of a = 7 m/s2.
Lesson 2.4 Recap
In this lesson we covered a framework for solving static and non-static force problems that involved only ONE object.
You practiced several questions to test your understanding and learned how to derive equations from scratch! Now you are ready to tackle questions involving all the other linear forces!
Lesson 2.5 Preview
In the next lesson ( Unit 2.5 – Tension and Elevators) we will cover the tension forces in depth, and how we can apply it to common scenarios like an elevator. We will also cover what apparent weight is and why it matters in elevators.


