What is Simple Harmonic Motion (SHM)?
SHM occurs when an object moves back and forth due to a restoring force that increases with displacement. For instance, in bungee jumping, the greater the stretch of the cord, the stronger the force pulling back.
💡 Restoring Force Can Vary!
- For a spring, the restoring force follows Hooke’s Law: \( F = -k x \).
- For a pendulum (and most other oscillating objects), the restoring force is a component of gravity: \( F = -mg \sin{\theta} \).
Key Idea: The force always pulls the object back to equilibrium and is proportional to displacement.
Period of Simple Harmonic Motion
Here are the key formulas for the period of a spring and pendulum system. We’ll also highlight some important insights that do and don’t affect the period of motion.
Spring-Mass System
For a mass on a spring the period is:
\[ T = 2\pi \sqrt{\frac{m}{k}} \]
- \(T\) = period (s)
- \(m\) = mass (kg)
- \(k\) = spring constant (N/m)
The amount a spring is stretched or compressed does not affect period. Thus, only the mass and spring constant affect the period.
Simple Pendulum
For a pendulum (assuming small angles) the period is:
\[ T = 2\pi \sqrt{\frac{\ell}{g}} \]
- \(T\) = period (s)
- \(\ell\) = length of the pendulum (m)
- \(g\) = \(9.81\) \(\text{m/s}^2\)
The mass of a pendulum doesn’t matter—only the length affects the period. Thus, a longer pendulum will swing more slowly.
📊 SHM Equations: Position, Velocity, and Acceleration
SHM is sinusoidal, meaning position, velocity, and acceleration all follow sine or cosine functions. The following 3 equations are the SHM equations:
Position Equation
The position of an object in SHM is given by:
\[ x = A \cos(\omega t) \quad \text{or} \quad x = A \sin(\omega t) \]
- \( x \) = position at time \( t \)
- \( A \) = amplitude (maximum displacement)
- \( \omega \) = angular frequency, measured in \(\text{rad/s}\)
Note on Angular Frequency \( \omega \)
\[ \omega = 2\pi f = \frac{2\pi}{T} \]
Where:
- \( \omega \) = angular frequency (radians per second)
- \( f \) = regular frequency (oscillations per second)
- \( T \) = period (time for one full oscillation)
You can extract the Period from \( \omega \) like this: \[ T = \frac{2\pi}{\omega} \]
Velocity Equation
Velocity in SHM is the derivative of the position equation. In other words, taking the slope of the SHM position equation gives us the velocity equation:
\[ v = -A \omega \sin(\omega t) \]
Max velocity is reached at the equilibrium position, where the object moves fastest. By applying the velocity equation, we can derive an expression for the maximum velocity:
\[ v_{\text{max}} = A \omega \]
Acceleration Equation
Acceleration in SHM is the derivative of velocity equation. In other words, taking the slope of the SHM velocity equation gives us the acceleration equation:
\[ a = -A \omega^2 \cos(\omega t) \]
In contrast to maximum velocity, maximum acceleration occurs at the maximum displacement. Utilizing the equation for acceleration, we can derive a formula for the maximum acceleration.
\[ a_{\text{max}} = A \omega^2 \]
💡 Amplitude \( A \) affects velocity and acceleration, but not period! A larger amplitude means bigger oscillations, but the time per cycle stays the same. This is also proven by the lack of amplitude in the period of a spring/pendulum equation.
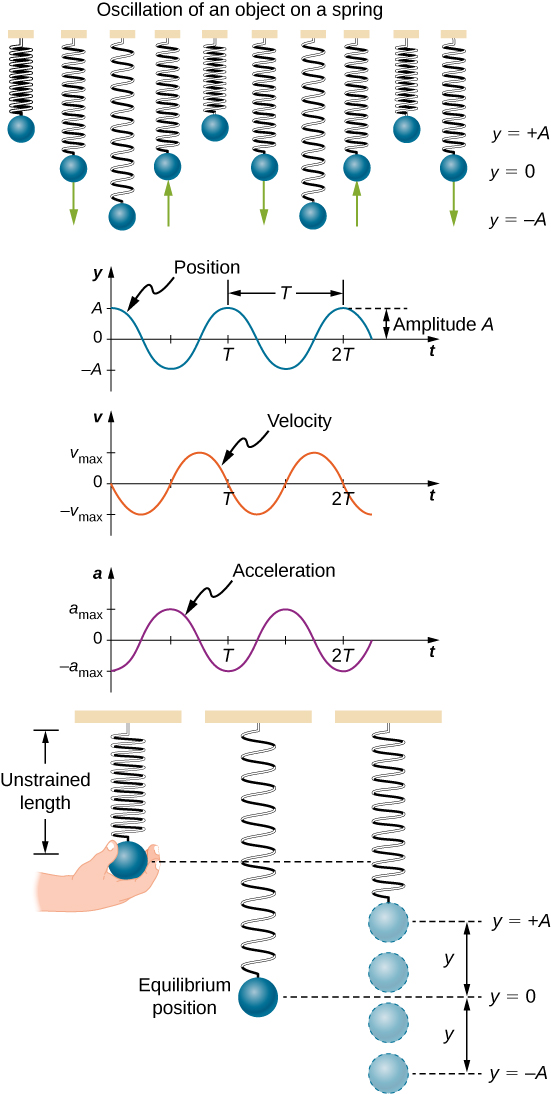
Visualizing SHM on graphs
SHM can be visualized with three key graphs: displacement, velocity, and acceleration vs. time by graphing the equations discussed above. To summarize:
| Graph Type | Key Characteristics |
|---|---|
| Displacement Graph (\(x\) vs. \(t\)) | The amplitude \( A \) is the max displacement from equilibrium (the x-axis). Period \( T \) is the time for one full cycle. |
| Velocity Graph (\(v\) vs. \(t\)) | Velocity is zero at max displacement (turning points). Velocity is maximum at equilibrium. |
| Acceleration Graph (\(a\) vs. \(t\)) | Acceleration is greatest at max displacement (strongest restoring force). Acceleration is zero at equilibrium. |
Visualizing the physical oscillation and graphs together
⚡ Energy in SHM
SHM always conserves mechanical energy, which swings between kinetic and potential energy:
\[ E_{\text{total}} = K + U \]
Energy in a Spring or Pendulum System
The total energy in a spring-mass system is:
\[ E_{\text{total}} = \frac{1}{2} k A^2 \]
The total energy in a pendulum-mass system is:
\[ E_{\text{total}} = mgh \]
or if given the maximum velocity for either spring or pendulum :
\[ E_{\text{total}} = \frac{1}{2} m v^2 \]
This is because:
- At max displacement, amplitude is a maximum and thus all energy is potential.
- At equilibrium, velocity is at a maximum and thus all energy is kinetic.
🧩 Common SHM Problems & How to Approach Them
Below we’ll cover commonly asked questions. Although we give equations to solve each, it’s expected that you know how to derive each formula below.
Note that these are just some of the questions you can be asked. So for quick and thorough mastery scroll down to the next part of this post for practice questions.
1. Finding Period & Frequency
What you need: Use the period equation for springs or pendulums.
You may also need to use this equation in conjunction with conservation of energy. i/.e: use the energy conservation to find spring constant \(k\) and then use that value in the period of a spring equation.
2. Finding Maximum Velocity or Acceleration Using the SHM equations
What you need:
\[ v_{\text{max}} = A \omega, \quad a_{\text{max}} = A \omega^2 \]
3. Energy Conservation in SHM
What you need: Use energy conservation \( E_{\text{initial}} = E_{\text{final}} \) to find velocity at a certain point.
4. Finding Speed at Equilibrium
What you need: Convert potential energy to kinetic energy:
\[ \frac{1}{2} k A^2 = \frac{1}{2} m v^2 \]
5. Acceleration at a Certain Displacement
Derive an equation using conservation of energy or forces. For example the acceleration of a mass on a spring at position \(x\) can be derived by setting the restoring force \(-kx\) equal to \(ma\):
\[ a = -\frac{k}{m} x \]
Like wise for a pendulum by setting the restoring force equal to \(ma\):
\[ a = -\frac{g}{L} x \]
📌 Final Takeaways (Cheat Sheet)
- SHM means energy is conserved—no external forces acting.
- Restoring force can be from a spring or gravity (pendulum).
- Amplitude \( A \) affects velocity and acceleration but not period.
- When it comes to SHM graphs/equations: Max velocity: \( v_{\text{max}} = A \omega \), Max acceleration: \( a_{\text{max}} = A \omega^2 \)
- Use period equations for timing problems.
- Use energy conservation for velocity-related problems.
- Use Newton’s Second Law for acceleration problems.
Practice Questions for Mastery
These are just a few SHM questions. For even more questions, detailed explanations, and automatic FRQ grading, check out UBQ. It’s free to use!
\( 4.8 \) \( \text{m} \)
\( 5.6 \) \( \text{m} \)
\( 3.7 \) \( \text{m} \)
\( 3.1 \) \( \text{m} \)
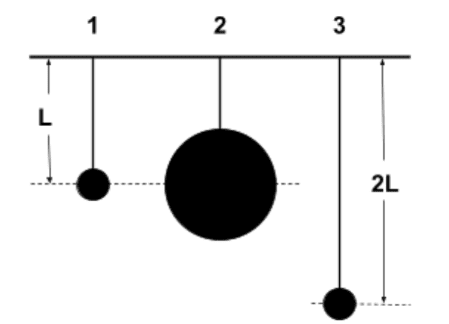Three pendulums are set in motion, oscillating through small amplitudes. Each has the same mass. Rank the period of the pendulums from shortest to longest.\(T_1 = T_2 = T_3\)
\(T_1 = T_2 > T_3\)
\(T_1 < T_2 < T_3\)
\(T_2 < T_1 < T_3\)
\(T_1 < T_2 = T_3\)
The speed is a maximum.
The potential energy is a minimum.
The speed is the minimum.
The restoring force is a minimum.
The kinetic energy is the maximum.
\[ \frac{3}{4} F_0 \]
\[ F_0 \]
\[ \frac{4}{3} F_0 \]
The answer cannot be determined without knowing the rock’s volume.
A simple pendulum oscillates with amplitude [katex]A[/katex] and period [katex]T[/katex], as represented on the graph above. Which option bests represents the magnitude of the pendulum's velocity [katex]v[/katex] and acceleration [katex]a[/katex] at time [katex] \frac{T}{2} [/katex]?[katex]v < 0, a < 0 [/katex]
[katex]v < 0, a = 0 [/katex]
[katex]v < 0, a > 0 [/katex]
[katex]v = 0, a > 0 [/katex]
[katex]v = 0, a = 0 [/katex]
