Finding tension in the string
| Step | Formula Derivation | Reasoning |
|---|---|---|
| 1 | \tan(\theta) = \frac{R}{h} | The angle \theta is between the string and the vertical axis. h is the vertical distance from the ball to the pivot. |
| 2 | h = L \cos(\theta) | From the geometry of the cone. |
| 3 | \tan(\theta) = \frac{R}{L \cos(\theta)} | Substituting the expression for h. |
| 4 | \sin(\theta) = \frac{R}{\sqrt{R^2 + h^2}} | From the right triangle formed by the string, h, and R. |
| 5 | F_{T} \sin(\theta) = F_{c} | The horizontal component of tension provides the centripetal force (F_{c}). |
| 6 | F_{c} = m \frac{v^2}{R} | Centripetal force formula. v is the velocity of the ball. |
| 7 | F_{T} \cos(\theta) = mg | The vertical component of tension balances gravity. |
| 8 | F_{T} = \frac{mg}{\cos(\theta)} | Isolating F_{T} in the vertical balance. |
| 9 | F_{T} = \frac{mg}{\cos(\theta)} = \frac{mg}{\sqrt{1 – \sin^2(\theta)}} | Using \cos(\theta) = \sqrt{1 – \sin^2(\theta)}. |
| 10 | F_{T} = \frac{mg}{\sqrt{1 – \left(\frac{R}{\sqrt{R^2 + h^2}}\right)^2}} | Substituting \sin(\theta). |
| 11 | \boxed{F_{T} = \frac{mg}{\sqrt{1 – \frac{R^2}{R^2 + L^2 \cos^2(\theta)}}}} | Final expression for tension, substituting h = L \cos(\theta). |
Finding period of the pendulum
| Step | Formula Derivation | Reasoning |
|---|---|---|
| 1 | F_{c} = m \frac{v^2}{R} | Centripetal force formula. |
| 2 | F_{T} \sin(\theta) = m \frac{v^2}{R} | The horizontal component of tension provides the centripetal force. |
| 3 | v = R \omega | Relationship between linear velocity and angular velocity (\omega). |
| 4 | m \frac{(R \omega)^2}{R} = F_{T} \sin(\theta) | Substituting v with R \omega. |
| 5 | \omega^2 = \frac{F_{T} \sin(\theta)}{mR} | Isolating \omega^2. |
| 6 | \omega = \sqrt{\frac{g}{R \tan(\theta)}} | Using F_{T} \sin(\theta) = mg \sin(\theta) and simplifying. |
| 7 | T = \frac{2\pi}{\omega} | Period (T |
Phy can also check your working. Just snap a picture!
A 2.0 kg ball on the end of a 0.65 m long string is moving in a vertical circle. At the bottom of the circle, its speed is 4.0 m/s. Find the tension in the string.
On a harsh winter day, a 1500 kg vehicle takes a circular banked exit ramp (radius R = 150 m; banking angle of 10 degrees) at a speed of 30 mph, since the speed limit is 35 mph. However, the exit ramp is completely iced up (= frictionless). To make matters worse, a wind is blowing parallel to the ramp in a downward direction. The wind exerts a force of 3000 N. Under these conditions, can the driver continue to follow a safe horizontal circle on the exit ramp and stay below the speed limit? To convert mph into m/s use 1 mi = 1607 m and 1 hr is 3600 s.
A 5.0 g coin is placed 15 cm from the center of a turntable. The coin has coefficients of static and kinetic friction of µs = 0.80 and µk = 0.50. The turntable slowly speeds up to 60 rpm. Does the coin slide off the turntable?
A 2.00 x102 g block on a 50.0 cm long string swings in a circle on a horizontal, frictionless table at 75.0 rpm. What is the speed of block? What is the tension in the string?
A communications satellite orbits the Earth at an altitude of 35,000 km above the Earth’s surface. Take the mass of Earth to be 6 \times 10^{24} \text{ kg} the the radius of Earth to be 6.4 \times 10^6 \text{ m}. What is the satellite’s velocity?
By continuing you (1) agree to our Terms of Sale and Terms of Use and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
| Kinematics | Forces |
|---|---|
| \Delta x = v_i t + \frac{1}{2} at^2 | F = ma |
| v = v_i + at | F_g = \frac{G m_1m_2}{r^2} |
| a = \frac{\Delta v}{\Delta t} | f = \mu N |
| R = \frac{v_i^2 \sin(2\theta)}{g} |
| Circular Motion | Energy |
|---|---|
| F_c = \frac{mv^2}{r} | KE = \frac{1}{2} mv^2 |
| a_c = \frac{v^2}{r} | PE = mgh |
| KE_i + PE_i = KE_f + PE_f |
| Momentum | Torque and Rotations |
|---|---|
| p = m v | \tau = r \cdot F \cdot \sin(\theta) |
| J = \Delta p | I = \sum mr^2 |
| p_i = p_f | L = I \cdot \omega |
| Simple Harmonic Motion |
|---|
| F = -k x |
| T = 2\pi \sqrt{\frac{l}{g}} |
| T = 2\pi \sqrt{\frac{m}{k}} |
| Constant | Description |
|---|---|
| g | Acceleration due to gravity, typically 9.8 , \text{m/s}^2 on Earth’s surface |
| G | Universal Gravitational Constant, 6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2 |
| \mu_k and \mu_s | Coefficients of kinetic (\mu_k) and static (\mu_s) friction, dimensionless. Static friction (\mu_s) is usually greater than kinetic friction (\mu_k) as it resists the start of motion. |
| k | Spring constant, in \text{N/m} |
| M_E = 5.972 \times 10^{24} , \text{kg} | Mass of the Earth |
| M_M = 7.348 \times 10^{22} , \text{kg} | Mass of the Moon |
| M_M = 1.989 \times 10^{30} , \text{kg} | Mass of the Sun |
| Variable | SI Unit |
|---|---|
| s (Displacement) | \text{meters (m)} |
| v (Velocity) | \text{meters per second (m/s)} |
| a (Acceleration) | \text{meters per second squared (m/s}^2\text{)} |
| t (Time) | \text{seconds (s)} |
| m (Mass) | \text{kilograms (kg)} |
| Variable | Derived SI Unit |
|---|---|
| F (Force) | \text{newtons (N)} |
| E, PE, KE (Energy, Potential Energy, Kinetic Energy) | \text{joules (J)} |
| P (Power) | \text{watts (W)} |
| p (Momentum) | \text{kilogram meters per second (kgm/s)} |
| \omega (Angular Velocity) | \text{radians per second (rad/s)} |
| \tau (Torque) | \text{newton meters (Nm)} |
| I (Moment of Inertia) | \text{kilogram meter squared (kgm}^2\text{)} |
| f (Frequency) | \text{hertz (Hz)} |
General Metric Conversion Chart
Example of using unit analysis: Convert 5 kilometers to millimeters.
Start with the given measurement: \text{5 km}
Use the conversion factors for kilometers to meters and meters to millimeters: \text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}}
Perform the multiplication: \text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}} = 5 \times 10^3 \times 10^3 \, \text{mm}
Simplify to get the final answer: \boxed{5 \times 10^6 \, \text{mm}}
Prefix | Symbol | Power of Ten | Equivalent |
|---|---|---|---|
Pico- | p | 10^{-12} | 0.000000000001 |
Nano- | n | 10^{-9} | 0.000000001 |
Micro- | µ | 10^{-6} | 0.000001 |
Milli- | m | 10^{-3} | 0.001 |
Centi- | c | 10^{-2} | 0.01 |
Deci- | d | 10^{-1} | 0.1 |
(Base unit) | – | 10^{0} | 1 |
Deca- or Deka- | da | 10^{1} | 10 |
Hecto- | h | 10^{2} | 100 |
Kilo- | k | 10^{3} | 1,000 |
Mega- | M | 10^{6} | 1,000,000 |
Giga- | G | 10^{9} | 1,000,000,000 |
Tera- | T | 10^{12} | 1,000,000,000,000 |
The most advanced version of Phy. Currently 50% off, for early supporters.
per month
Billed Monthly. Cancel Anytime.
Trial –> Phy Pro
A quick explanation
UBQ credits are specifically used to grade your FRQs and GQs.
You can still view questions and see answers without credits.
Submitting an answer counts as 1 attempt.
Seeing answer or explanation counts as a failed attempt.
Lastly, check your average score, across every attempt, in the top left.
MCQs are 1 point each. GQs are 1 point. FRQs will state points for each part.
Phy can give partial credit for GQs & FRQs.
Phy sees everything.
It customizes responses, explanations, and feedback based on what you struggle with. Try your best on every question!
Understand you mistakes quicker.
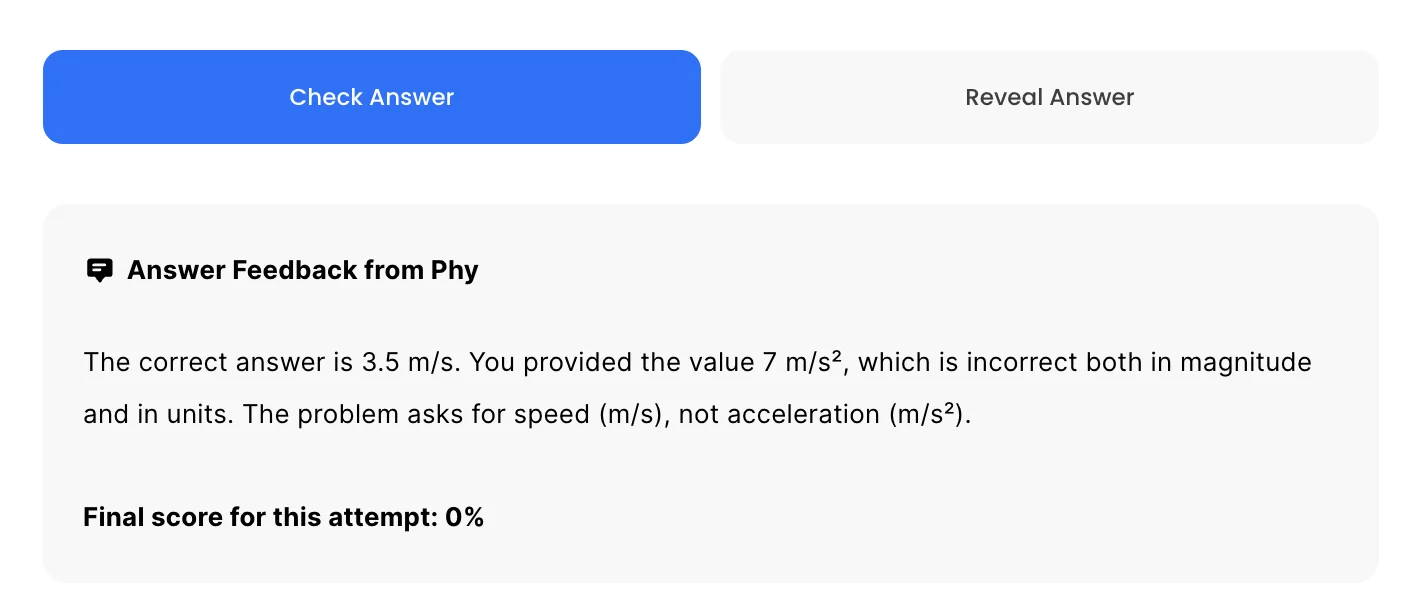
For GQs and FRQs, Phy provides brief feedback as to how you can improve your answer.
Aim to increase your understadning and average score with every attempt!
10 Free Credits To Get You Started
*Phy Pro members get unlimited credits
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.