Objective: Calculate the magnitude of the kinetic frictional force exerted on the fireman as he slides down the pole.
| Step | Formula Derivation | Reasoning |
|---|---|---|
| 1 | v^2 = u^2 + 2as | Kinematic equation relating initial velocity (u), final velocity (v), acceleration (a), and displacement (s). |
| 2 | a = \frac{v^2 – u^2}{2s} | Solve for acceleration (a). |
| 3 | a = \frac{(1.36\text{ m/s})^2 – 0}{2 \times 4.20\text{ m}} | Substitute u = 0 (starting from rest), v = 1.36\text{ m/s}, and s = 4.20\text{ m}. |
| 4 | a = \frac{1.8496\text{ m}^2/\text{s}^2}{8.40\text{ m}} | Calculate the numerator. |
| 5 | a = 0.22\text{ m/s}^2 | Calculate the acceleration. |
| 6 | F_{\text{net}} = ma | Newton’s second law. |
| 7 | F_{\text{net}} = 79.34\text{ kg} \times 0.22\text{ m/s}^2 | Substitute the mass (m) and acceleration (a). |
| 8 | F_{\text{net}} = 17.45\text{ N} | Calculate the net force. |
| 9 | F_{\text{friction}} = mg – F_{\text{net}} | The frictional force is the difference between gravitational force and net force. |
| 10 | F_{\text{friction}} = 79.34\text{ kg} \times 9.8\text{ m/s}^2 – 17.45\text{ N} | Substitute gravitational acceleration (g) and net force (F_{\text{net}}). |
| 11 | F_{\text{friction}} = 777.532\text{ N} – 17.45\text{ N} | Calculate the gravitational force. |
| 12 | F_{\text{friction}} = 760\text{ N} | Calculate the frictional force. |
Final answer for the magnitude of the kinetic frictional force: \boxed{F_{\text{friction}} = 760\text{ N}}
Phy can also check your working. Just snap a picture!
The coefficient of kinetic friction is
A person is trying to judge whether a picture (mass = 1.42 kg) is properly positioned by temporarily pressing it against a wall. The pressing force is perpendicular to the wall. The coefficient of static friction between the picture and the wall is 0.62. What is the minimum amount of pressing force that must be used?
A car slides up a frictionless inclined plane. How does the normal force of the incline on the car compare with the weight of the car?
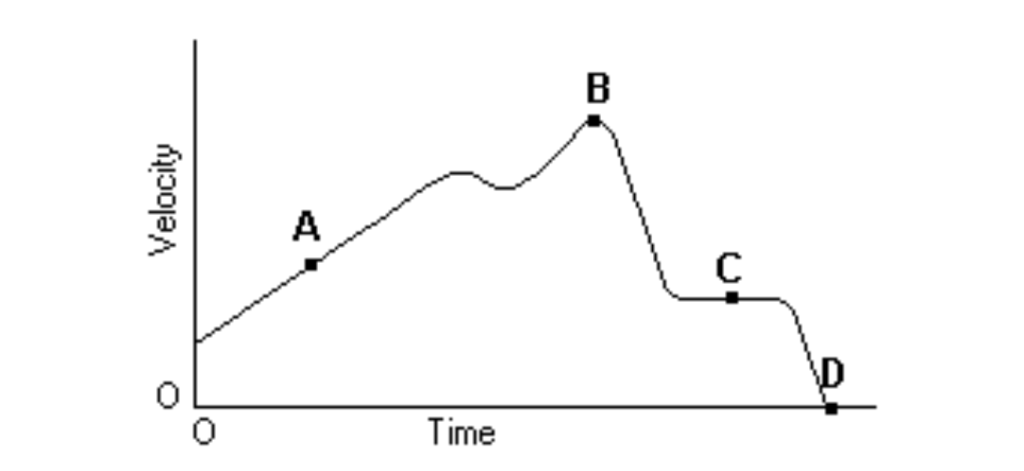 Above is the graph of the velocity vs. time of a duck flying due south for the winter. At what point might the duck begin reversing directions?
Above is the graph of the velocity vs. time of a duck flying due south for the winter. At what point might the duck begin reversing directions?
A cart with an initial velocity of 5.0 m/s to the right experiences a constant acceleration of 2.0 m/s2 to the right. What is the cart’s displacement during the first 6.0 s of this motion?
760 N
By continuing you (1) agree to our Terms of Sale and Terms of Use and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
| Kinematics | Forces |
|---|---|
| \Delta x = v_i t + \frac{1}{2} at^2 | F = ma |
| v = v_i + at | F_g = \frac{G m_1m_2}{r^2} |
| a = \frac{\Delta v}{\Delta t} | f = \mu N |
| R = \frac{v_i^2 \sin(2\theta)}{g} |
| Circular Motion | Energy |
|---|---|
| F_c = \frac{mv^2}{r} | KE = \frac{1}{2} mv^2 |
| a_c = \frac{v^2}{r} | PE = mgh |
| KE_i + PE_i = KE_f + PE_f |
| Momentum | Torque and Rotations |
|---|---|
| p = m v | \tau = r \cdot F \cdot \sin(\theta) |
| J = \Delta p | I = \sum mr^2 |
| p_i = p_f | L = I \cdot \omega |
| Simple Harmonic Motion |
|---|
| F = -k x |
| T = 2\pi \sqrt{\frac{l}{g}} |
| T = 2\pi \sqrt{\frac{m}{k}} |
| Constant | Description |
|---|---|
| g | Acceleration due to gravity, typically 9.8 , \text{m/s}^2 on Earth’s surface |
| G | Universal Gravitational Constant, 6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2 |
| \mu_k and \mu_s | Coefficients of kinetic (\mu_k) and static (\mu_s) friction, dimensionless. Static friction (\mu_s) is usually greater than kinetic friction (\mu_k) as it resists the start of motion. |
| k | Spring constant, in \text{N/m} |
| M_E = 5.972 \times 10^{24} , \text{kg} | Mass of the Earth |
| M_M = 7.348 \times 10^{22} , \text{kg} | Mass of the Moon |
| M_M = 1.989 \times 10^{30} , \text{kg} | Mass of the Sun |
| Variable | SI Unit |
|---|---|
| s (Displacement) | \text{meters (m)} |
| v (Velocity) | \text{meters per second (m/s)} |
| a (Acceleration) | \text{meters per second squared (m/s}^2\text{)} |
| t (Time) | \text{seconds (s)} |
| m (Mass) | \text{kilograms (kg)} |
| Variable | Derived SI Unit |
|---|---|
| F (Force) | \text{newtons (N)} |
| E, PE, KE (Energy, Potential Energy, Kinetic Energy) | \text{joules (J)} |
| P (Power) | \text{watts (W)} |
| p (Momentum) | \text{kilogram meters per second (kgm/s)} |
| \omega (Angular Velocity) | \text{radians per second (rad/s)} |
| \tau (Torque) | \text{newton meters (Nm)} |
| I (Moment of Inertia) | \text{kilogram meter squared (kgm}^2\text{)} |
| f (Frequency) | \text{hertz (Hz)} |
General Metric Conversion Chart
Example of using unit analysis: Convert 5 kilometers to millimeters.
Start with the given measurement: \text{5 km}
Use the conversion factors for kilometers to meters and meters to millimeters: \text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}}
Perform the multiplication: \text{5 km} \times \frac{10^3 \, \text{m}}{1 \, \text{km}} \times \frac{10^3 \, \text{mm}}{1 \, \text{m}} = 5 \times 10^3 \times 10^3 \, \text{mm}
Simplify to get the final answer: \boxed{5 \times 10^6 \, \text{mm}}
Prefix | Symbol | Power of Ten | Equivalent |
|---|---|---|---|
Pico- | p | 10^{-12} | 0.000000000001 |
Nano- | n | 10^{-9} | 0.000000001 |
Micro- | µ | 10^{-6} | 0.000001 |
Milli- | m | 10^{-3} | 0.001 |
Centi- | c | 10^{-2} | 0.01 |
Deci- | d | 10^{-1} | 0.1 |
(Base unit) | – | 10^{0} | 1 |
Deca- or Deka- | da | 10^{1} | 10 |
Hecto- | h | 10^{2} | 100 |
Kilo- | k | 10^{3} | 1,000 |
Mega- | M | 10^{6} | 1,000,000 |
Giga- | G | 10^{9} | 1,000,000,000 |
Tera- | T | 10^{12} | 1,000,000,000,000 |
The most advanced version of Phy. Currently 50% off, for early supporters.
per month
Billed Monthly. Cancel Anytime.
Trial –> Phy Pro
A quick explanation
UBQ credits are specifically used to grade your FRQs and GQs.
You can still view questions and see answers without credits.
Submitting an answer counts as 1 attempt.
Seeing answer or explanation counts as a failed attempt.
Lastly, check your average score, across every attempt, in the top left.
MCQs are 1 point each. GQs are 1 point. FRQs will state points for each part.
Phy can give partial credit for GQs & FRQs.
Phy sees everything.
It customizes responses, explanations, and feedback based on what you struggle with. Try your best on every question!
Understand you mistakes quicker.
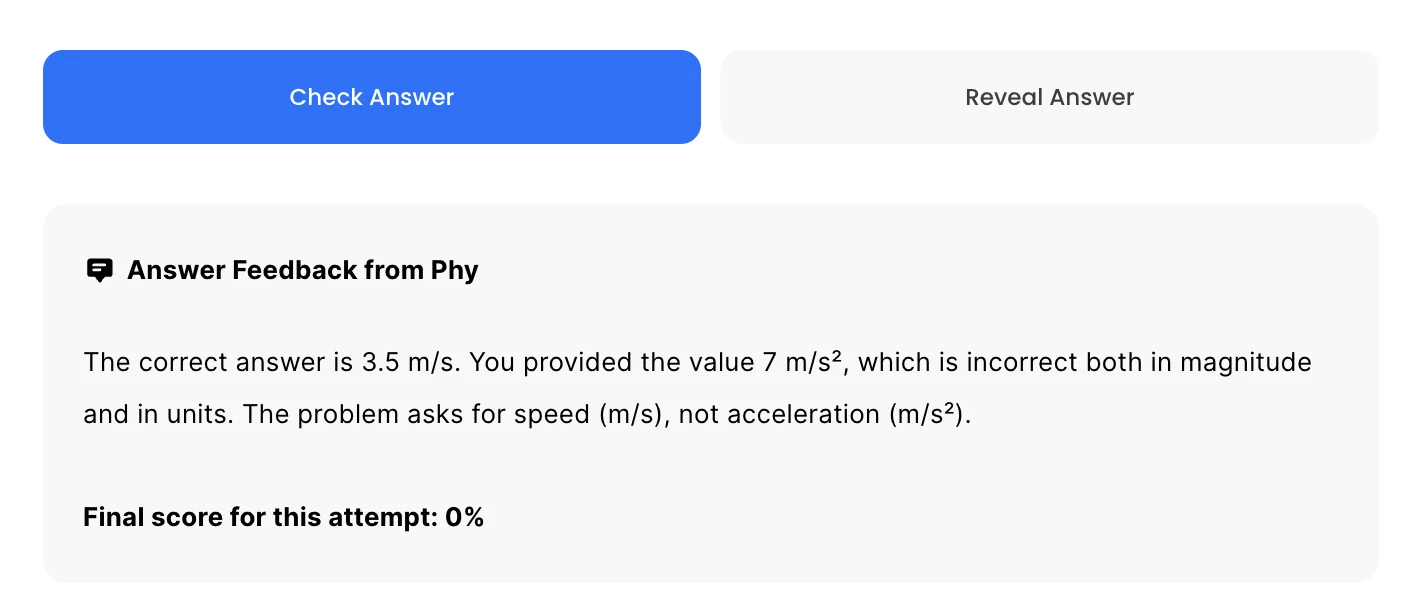
For GQs and FRQs, Phy provides brief feedback as to how you can improve your answer.
Aim to increase your understadning and average score with every attempt!
10 Free Credits To Get You Started
*Phy Pro members get unlimited credits
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.