🚀 AP Physics 1: The Ultimate Fluids Speed Review
So, fluids made the cut for AP Physics 1. Great. Another topic to cram.
But don’t worry—this guide will get you up to speed with everything you need to know about fluids, pressure, buoyancy, and flow, minus the fluff. Let’s get into it.
💡 First Things First: What Even is a Fluid?
Fluids are anything that flows—liquids, gases, and whatever weird in-between states physics hasn’t classified yet. Unlike solids, fluids don’t hold their shape; they take the form of whatever container they’re in.
The key quantity to track? Density, which is just mass packed into a given volume:
\[ \rho = \frac{m}{V} \]
Think about it: oil floats on water because it’s less dense. Helium rises in air for the same reason. Simple.
🔧 Pressure: The Invisible Force You Never Notice
Pressure is how much force a fluid applies over an area. Mathematically, that’s:
\[ P = \frac{F_{\perp}}{A} \]
More force? More pressure. Smaller area? Even more pressure. That’s why a sharp knife cuts better than a dull one.
📝 A Note on Pascal’s Law
Normally, this is where we’d talk about Pascal’s Law—the principle that explains how a change in pressure is transmitted equally throughout a fluid.
This is the reason hydraulic systems work, like the braking system in your car. A small force applied at one end can create a much larger force at the other, making it possible to stop a car with just the pressure from your foot.
The equation for Pascal’s Law is:
\[ F_1 = \frac{A_1}{A_2} F_2 \]
Although Nerd Notes includes Pascal’s Law in our practice question bank under fluids, it’s important to note that this is not covered on the AP Physics 1 exam. The exam only tests concepts related to fluid pressure, which we’ll focus on next.
⏬ How Fluid Pressure Changes with Depth
Go deeper underwater, and pressure increases. The equation for absolute pressure is:
\[ P = P_0 + \rho gh \]
Where \(P_0\) is atmospheric pressure at the surface, and \(\rho gh\) is the extra pressure from the fluid above you.
That’s why deep-sea fish look like nightmares—high pressure squashes anything that isn’t built for it.
⚖️ Buoyancy: Why Some Things Float and Others Sink
Ever tried to push a beach ball underwater? The harder you push, the stronger the water pushes back. That’s buoyancy in action.
Archimedes figured out that the buoyant force equals the weight of the displaced fluid:
\[ F_b = \rho V g \]
If \(F_b\) is greater than the object’s weight, it floats. If not, down it goes.
This also explains why ships, despite being made of heavy metal, don’t sink—because they displace enough water to generate a buoyant force greater than their own weight.
🚰 Fluid Flow: The Traffic Laws of Physics
Fluids follow a strict rule: what goes in must come out. That’s where the continuity equation comes in:
\[ A_1 v_1 = A_2 v_2 \]
Here’s what it really means: the volume of fluid flowing per second stays the same, no matter how the pipe’s shape changes. This is called the flow rate (\( Q \)), defined as:
\[ Q = A v \]
Where:
- \(Q\) = flow rate (m³/s)
- \(A\) = cross-sectional area (m²)
- \(v\) = velocity of the fluid (m/s)
If a pipe gets narrower, the velocity increases to maintain the same flow rate. If it widens, the velocity decreases. That’s why river rapids form when a wide river suddenly narrows—water speeds up to keep the same volume moving through.
💡 Key takeaway: The flow rate always stays constant for an incompressible fluid. If area changes, velocity adjusts to compensate.
🛫 Bernoulli’s Equation: Why Airplanes Fly
Bernoulli’s principle is just conservation of energy applied to fluids. It states that a fluid’s total energy (pressure, gravitational potential, and kinetic) stays constant:
\[ P_1 + \rho g y_1 + \frac{1}{2} \rho v_1^2 = P_2 + \rho g y_2 + \frac{1}{2} \rho v_2^2 \]
This explains:
- How airplanes generate lift (faster air = lower pressure)
- Why a shower curtain gets sucked inward when you turn on the water
- How a perfume atomizer sprays liquid
🚀 Torricelli’s Theorem: Fluid Speed Without the Drama
When a fluid drains out of a hole, it acts like it’s in free fall. Torricelli’s equation gives its speed:
\[ v = \sqrt{2g\Delta y} \]
The greater the height difference, the faster the fluid moves. That’s why water from a tall tower shoots out faster than from a short one.
📌 Final Takeaways (a.k.a. Your Cheat Sheet)
- Pressure increases with depth: \( P = P_0 + \rho gh \)
- Buoyant force = weight of displaced fluid: \( F_b = \rho V g \)
- Fluid flow speeds up in narrow spaces: \( A_1 v_1 = A_2 v_2 \)
- Fast-moving fluids have low pressure: Bernoulli’s equation
- Fluid draining from a hole follows \( v = \sqrt{2g\Delta y} \)
Master these, and you’ll crush any fluids question the AP throws at you.
If you’re looking for free fluid practice questions in AP style, check out UBQ, our collection of over 1000+ Physics questions, with explanations, AI powered assistance, and automatic FRQ grading. Over 200,000 students use it daily to accelerate this success! Try it here.
Practice Questions for Mastery
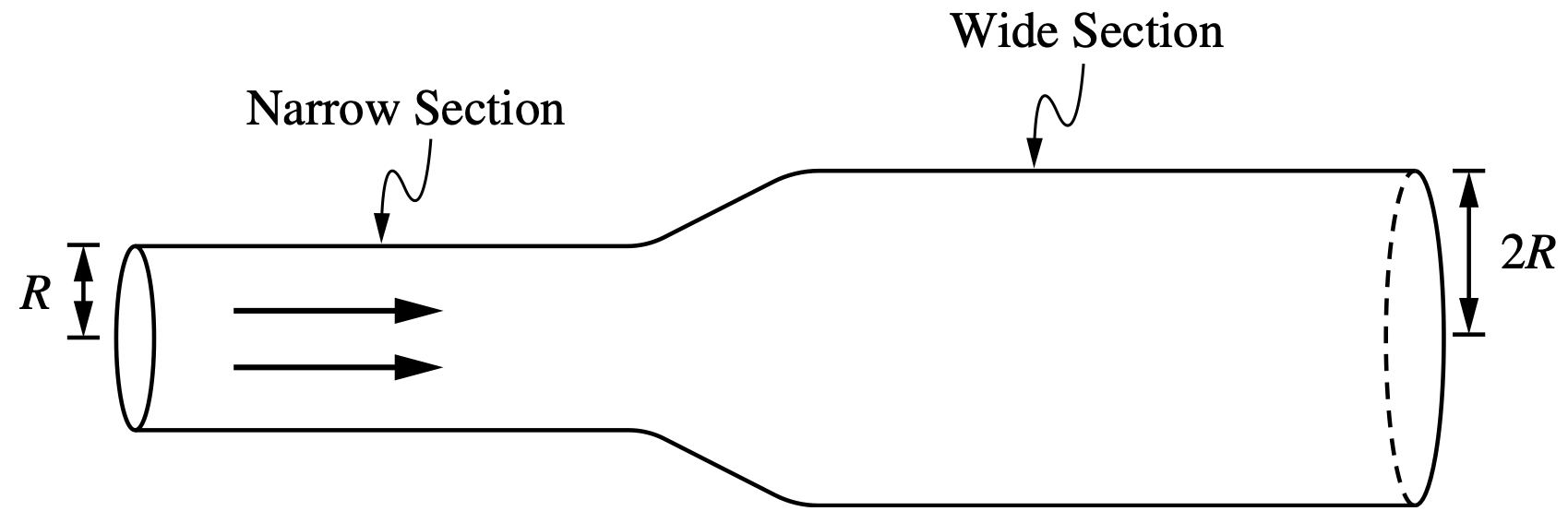A fluid flows through the two sections of cylindrical pipe shown in the figure. The narrow section of the pipe has radius \( R \) and the wide section has radius \( 2R \). What is the ratio of the fluid’s speed in the wide section of pipe to its speed in the narrow section of pipe, \( \frac{v_{\text{wide}}}{v_{\text{narrow}}} \)?\[ \frac{1}{4} \]
\[ \frac{1}{2} \]
\[ 2 \]
\[ 4 \]
\[ \frac{3}{4} F_0 \]
\[ F_0 \]
\[ \frac{4}{3} F_0 \]
The answer cannot be determined without knowing the rock’s volume.
