Are astronauts really “weightless” while in orbit?
A spring is connected to a wall and a horizontal force of \( 80.0 \) \( \text{N} \) is applied. It stretches \( 25 \) \( \text{cm} \); what is its spring constant?
A satellite in circular orbit around the Earth moves at constant speed. This orbit is maintained by the force of gravity between the Earth and the satellite, yet no work is done on the satellite. How is this possible?
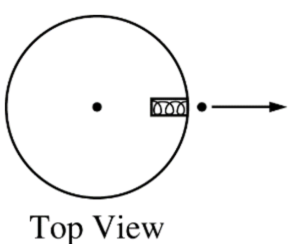
A compressed spring mounted on a disk can project a small ball. When the disk is not rotating, as shown in the top view above, the ball moves radially outward. The disk then rotates in a counterclockwise direction as seen from above, and the ball is projected outward at the instant the disk is in the position shown above. Which of the following best shows the subsequent path of the ball relative to the ground?

A block of mass \( 0.5 \) \( \text{kg} \) is attached to a horizontal spring with a spring constant of \( 150 \) \( \text{N/m} \). The block is released from rest at position \( x = 0.05 \) \( \text{m} \), as shown, and undergoes simple harmonic motion, reaching a maximum position of \( x = 0.1 \) \( \text{m} \). The speed of the block when it passes through position \( x = 0.09 \) \( \text{m} \) is most nearly
A car increases its forward velocity uniformly from \(40 ~ \text{m/s}\) to \(80 ~ \text{m/s}\) while traveling a distance of \(200 ~ \text{m}\). What is its acceleration during this time?
The heaviest train ever pulled by a single engine was over [katex] 2 \, \text{km} [/katex] long. A force of [katex] 1.13 \times 10^5 \, \text{N} [/katex] is needed to get the train to start moving. If the coefficient of static friction is [katex] 0.741 [/katex] and the coefficient of kinetic friction is [katex] .592 [/katex], what is the train’s mass?
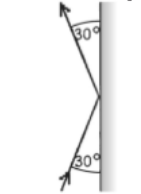
A super dart of mass \(20 \, \text{g}\), traveling at \(350 \, \text{m/s}\), strikes a steel plate at an angle of \(30^\circ\) with the plane of the plate, as shown in the figure. It bounces off the plate at the same angle but at a speed of \(320 \, \text{m/s}\). What is the magnitude of the impulse that the plate gives to the bullet?
Which of the following must be zero if an object is spinning at a constant rate? There may be more than one right answer.
A cannon fires projectiles on a flat range at a fixed speed but with variable angle. The maximum range of the cannon is \(L\). What is the range of the cannon when it fires at an angle of \(30^\circ\) above the horizontal? Ignore air resistance.
A \( 1.5 \; \text{kg} \) mass attached to a spring with a force constant of \( 20.0 \; \text{N/m} \) oscillates on a horizontal, frictionless track. At \( t = 0 \), the mass is released from rest at \( x = 10.0 \; \text{cm} \). (That is, the spring is stretched by \( 10.00 \; \text{cm} \).)
What is the effect on the period of a pendulum if you double its length?
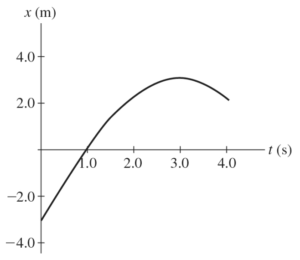
The graph in the figure shows the position of a particle as it travels along the x-axis. At what value of \(t\) is the speed of the particle equal to \(0 \, \text{m/s}\)?
note that the slope of position vs time is velocity. And the graph most closely reemsbles a flat or 0 slope at 3 seconds
A rotating merry-go-round makes one complete revolution in 4.0 s. What is the linear speed and acceleration of a child seated 1.2 m from the center?
An \( 80 \, \text{kg} \) block is placed \( 2 \, \text{m} \) away from the endpoint of a horizontal steel beam of length \( 6.6 \, \text{m} \) and mass \( 1,450 \, \text{kg} \). The plank makes contact with a vertical wall on one end (assume it does not slip). The other end of the beam is attached to a massless cable that makes an angle of \( 30^\circ \) with the horizontal and ties into the vertical wall as well. Calculate the (1) tension force in the cable and (2) the total force the wall exerts on the beam.
A cardinal (Richmondena cardinalis) of mass \( 3.80 \times 10^{-2} \) \( \text{kg} \) and a baseball of mass \( 0.150 \) \( \text{kg} \) have the same kinetic energy. What is the ratio of the cardinal’s magnitude \( p_c \) of momentum to the magnitude \( p_b \) of the baseball’s momentum?
You stand at the edge of a vertical cliff and throws a stone vertically upwards. The stone leaves your hand with a speed v = 8.0 m/s. The time between the stone leaving your hand and hitting the sea is 3.0 s. Assume air resistance is negligible. Calculate:
By continuing you (1) agree to our Terms of Use and Terms of Sale and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
Quick Start Guide
AP physics 1, AP C, honors and advanced physics students.
Quickly filter questions by units and more.


Here’s guide to using 5 UBQ filters.
GQ = general question, MCQ = multiple choice, FRQ = free response.

Click the check or bookmark button.
Now you’ll be able to see completed or bookmarked questions at a glance!
Answer keys, personalized for you.
Phy will be responsible for grading your FRQs and GQs.
No more copy and pasting. Just solve and snap.
Questions for Mastery
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.