A 2.2 kg ball on the end of a 0.35 m long string is moving in a vertical circle. At the bottom of the circle, its speed is 5.3 m/s. Find the tension in the string.
A \( 50 \) \( \text{g} \) ice cube can slide up and down a frictionless \( 30^{\circ}\) slope. At the bottom, a spring with spring constant \( 25 \) \( \text{N/m} \) is compressed \( 10 \) \( \text{cm} \) and is used to launch the ice cube up the slope. How high does it go above its starting point? Express your answer with the appropriate units.
A snowboarder starts from rest and slides down a \(32^\circ\) incline that’s \(75 \, \text{m}\) long.
A block sliding down an frictionless inclined plane is experiencing both gravitational and normal forces; which force’s magnitude changes when the angle of the incline is increased?
The International Space Station travels at \( 7660 \, \text{m/s} \). Find the average velocity of the space station if it takes \( 90 \, \text{minutes} \) to make one full orbit around Earth.
An object undergoes constant acceleration. Starting from rest, the object travels \( 5 \, \text{m} \) in the first second. Then it travels \( 15 \, \text{m} \) in the next second. What total distance will be covered after the 3rd second?
A cardinal (Richmondena cardinalis) of mass \( 3.80 \times 10^{-2} \) \( \text{kg} \) and a baseball of mass \( 0.150 \) \( \text{kg} \) have the same kinetic energy. What is the ratio of the cardinal’s magnitude \( p_c \) of momentum to the magnitude \( p_b \) of the baseball’s momentum?
A uniform rope of weight \( 30 \, \text{N} \) hangs from a hook. A box of mass \( 40 \, \text{kg} \) is suspended from the rope. What is the tension in the rope?
In the absence of air resistance, a projectile is launched from and returns to ground level and has a range of \( 23 \, \text{m} \). Suppose the launch speed is doubled, and the projectile is fired at the same angle above the ground. What is the new range?
Two blocks connected to a compressed spring move right at speed v. After releasing the spring, the left block moves left at speed [katex] v_2 [/katex], the right block moves right. What is the center speed of the blocks then?
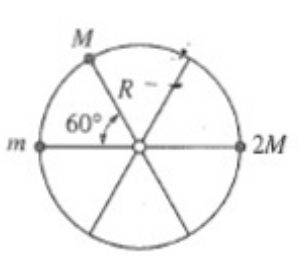
A wheel of radius \( R \) and negligible mass is mounted on a horizontal frictionless axle so that the wheel is in a vertical plane. Three small objects having masses \( m \), \( M \), and \( 2M \), respectively, are mounted on the rim of the wheel, as shown above. If the system is in static equilibrium, what is the value of \( m \) in terms of \( M \)?
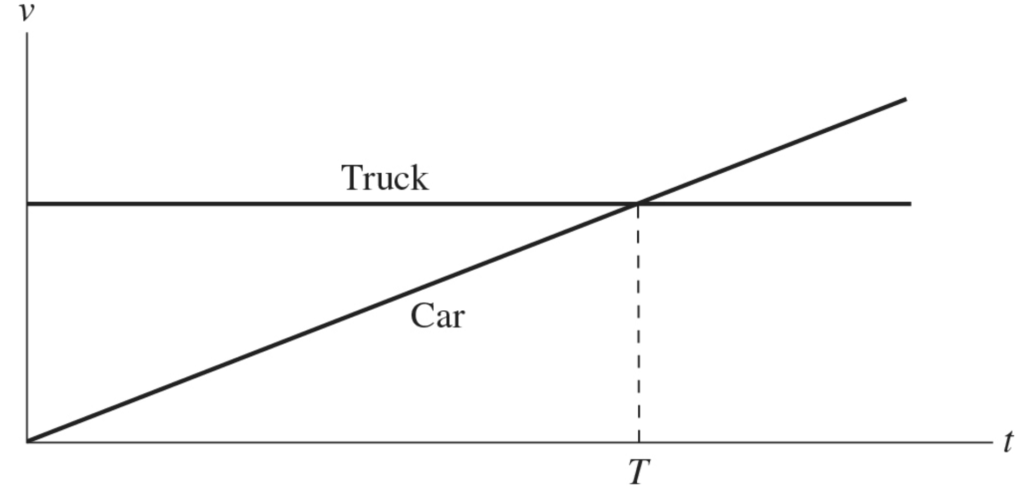
The motions of a car and a truck along a straight road are represented by the velocity–time graphs in the figure. The two vehicles are initially alongside each other at time \(t = 0\). At time \(T\), what is true of the distances traveled by the vehicles since time \(t = 0\)?
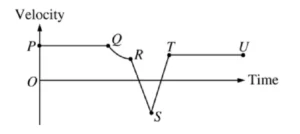The graph above shows velocity as a function of time for an object moving along a straight line. For which of the following sections of the graph is the acceleration constant and nonzero?
What does displacement mean in the context of motion?
A block of weight \( W \) is pulled along a horizontal surface at constant speed by a force \( F \), which acts at an angle of \( \theta \) with the horizontal. The normal force exerted on the block by the surface has magnitude:
Which of the following must be true for an object at translational equilibrium?
Two closed containers look the same, but one is packed with lead and the other with a few feathers. How could you determine which has more mass if you and the containers were orbiting in a weightless condition in outer space?
An object is moving to the west at a constant speed. Three forces are exerted on the object. One force is \( 10 \) \( \text{N} \) directed due north, and another is \( 10 \) \( \text{N} \) directed due west. What is the magnitude and direction of the third force if the object is to continue moving to the west at a constant speed?
By continuing you (1) agree to our Terms of Use and Terms of Sale and (2) consent to sharing your IP and browser information used by this site’s security protocols as outlined in our Privacy Policy.
Here’s guide to using 5 UBQ filters.
GQ = general question, MCQ = multiple choice, FRQ = free response.
Click the check or bookmark button.
Now you’ll be able to see completed or bookmarked questions at a glance!
Answer keys, personalized for you.
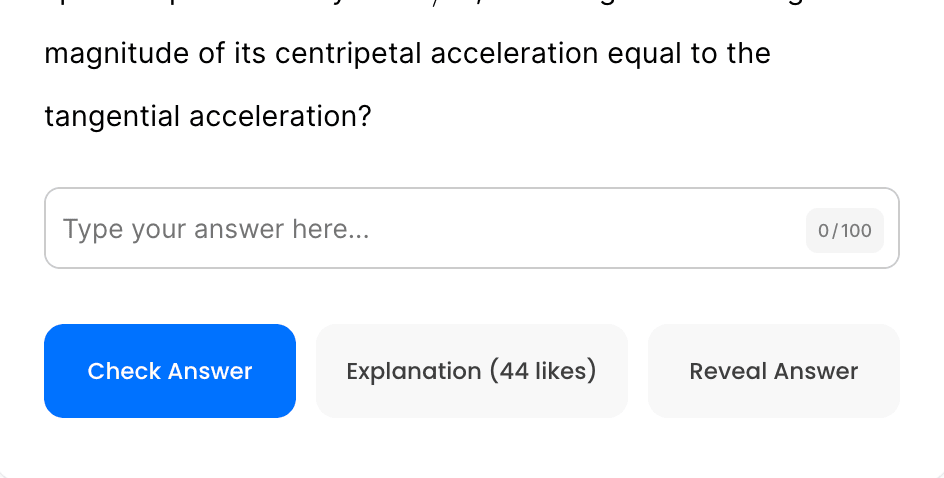
Phy will be responsible for grading your FRQs and GQs.
No more copy and pasting. Just solve and snap.
Questions for Mastery
By continuing you agree to nerd-notes.com Terms of Service, Privacy Policy, and our usage of user data.
