Unit 1 Breakdown
You are on Lesson 1 of 5
- Unit 1.1 | Understanding vectors and the standard units used in Physics [Current lesson]
- Unit 1.2 The kinematic (motion) variables: Displacement, velocity, and acceleration
- Unit 1.3 | Graphing motion
- Unit 1.4 | Using kinematic equations in 1 dimension
- Unit 1.5 | Projectile motion: Using kinematic equations in 2 dimensions
In this lesson you will learn
- Kinematics – what it is?
- Vectors – what they are and how/why we use them in Physics
- Vector manipulation – adding and splitting up vectors
- Units – motion graphs and equations
Introduction
Hello, young physicists! Welcome to the exciting world of physics. We will embark on a journey to understand the universe and the principles that govern it.
Kinematics, or the study of motion, is the first part of this journey.
It makes up 12-18% of the AP Physics 1 content. Or around 10% of a regular Physics curriculum.
In order to understand Kinematics (and the rest of Physics) we must first cover 2 important topics: Vectors and Standard Units.
What are Vectors?
Vectors are simply arrows! They will be used EVERYWHERE in physics, not just kinematics.
Vectors have two things: a length (also called a magnitude or scalar) and a direction.
This is how to write a vector: \vec{A}.
This is how to write a scalar: A OR \lvert \vec{A} \rvert.
Length and Direction
The length can represent anything like distance, speed, forces, and more.
And the direction can be given as any of the 4 things below:
Vector example: riding on a bike at 5 m/s north. Notice how BOTH the magnitude (5 miles) AND the direction (north) is specified.
Vectors vs Scalars
| Scalar (just a number) | Vector (number and a direction) |
| volume (1 liter) | – |
| time (30 seconds) | acceleration due to gravity (-9.81 m/s2) |
| distance (10 feet) | displacement (10 feet north-west) |
| speed (100 km/hr) | velocity (100 km/hr south) |
| mass (25 kg) | force (15 Newtons, 30° above the horizontal) |
Why Vectors
You might be wondering where and why we use vectors in physics.
Using vectors allows us to view motion in multiple directions.
Look at the image below. The soccer ball is kicked at a velocity v_0 that is 30º above the soccer field.
Note that velocity means speed and v_0 is the variable for “initial velocity.” It is a placeholder for the numerical value of the velocity of the soccer ball.
Physicists can take the v_0 velocity vector and separate it into two parts: the H vector and the R vector as shown in the image above. These are what we call vector components.
Vector Components
Since we can break 1 vector down into 2 components of this motion, we can see that the ball is really moving both up and to the right at the same time.
We can use these components (or parts of the velocity vector) to solve real world problems, like how far did the ball travel before landing on the ground?
LRN Vector Math
In Physics, there are 4 things you will be doing with vectors. The most important one is the last one and there is a short video below showing how to do it.
- number \times \vec {A} : Multiply a vector by a scalar to increase the size the of the vector.
- \vec{A} + \vec{B} : Add two vectors along the same axis to get a resultant vector.
- \vec{A} \times \vec{B} : Add two perpendicular vectors to get a resultant vector.
- \vec{A} = \vec{A_x} \times \vec{A_y} : Take 1 vector and break it down into the horizontal and vertical components
Okay now that you what we can do with vectors, lets put into practice! Watch the short video below, and try the example problems after.
PQ Vector Components
After watching the video above you should have a solid understanding of adding vectors and breaking them into components. Attempt all the practice questions below and be sure to understand all missed ones before moving on.
(1) Find the resultant vector (magnitude AND direction) given the following components:
- Ax = 5.7, Ay = 3.2; Answer: (A = 6.6 at 30.8 degrees above the +x axis)
- Bx = -10, By = -3; Answer: (B = 10.4 at 16.7 degrees below the -x axis)
- Cx = 11.65, Cy = -20.17; Answer: (C = 23.3 at 60 degrees below the +x axis)
(2) Find the X and Y components of the following vectors:
- 35 m/s at 57° from the x-axis; Answer: (X: 19.1 m/s, Y: 29.4 m/s)
- 12 m/s at 34° S of W; Answer: (X: -10 m/s, Y: -6.7 m/s)
- 20 m/s 275° from the x-axis; Answer: (X: 1.75 m/s, Y: -20 m/s)
- A plane takes off with a velocity, v, of 40 m/s at an angle of 15° above the ground; Answer: (vx = 38.6 m/s, vy: 10.4 m/s)
(3) Challenge: Listed below are 4 distance vectors.
- A: 15 m at 60° above the +x-axis
- B: 10 m east
- C: 25 m south
- D: 50 meters at 28° South of West
Using the vectors above, preform the following operations:
- A + B + C + D; Answer: (29 m at 23° above the -x-axis or 23° N of W)
- A – C; Answer: (38.7 m at 78.8° above the +x-axis or 78° N of E)
- D + 2C; Answer: (51.4 m at 31° below the -x-axis or 31° S of W)
Hint: Draw out each vector on a graph. Break each vector into x and y components, then preform the operations in each direction.
Using the Standard Units of Measurement
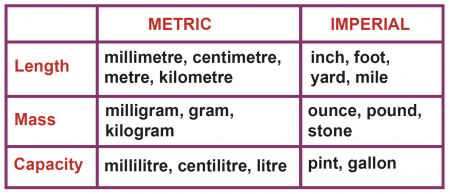
If you’re from the United States you may be used to seeing miles, miles per hour, feet, pounds etc.
This is the imperial system of measurement. And it makes calculations and conversions difficult.
Instead, in physics, we use the metric system (kilometers, meters, kilograms, etc) that the rest of the world is familiar with.
Why Metric?
The metric system is much easier to convert between orders of magnitude.
For example, how many centimeters are in a meter? Well we can simply look at the prefix “centi” and tell that there are 100 centimeters in 1 meter.
So in Physics, you’ll commonly see the following standard units:
- Distance is measured in meters (m)
- Speed is measured in meters per second (m/s)
- Weight is measured in kilograms (kg)
- Time is measured in seconds (s)
From now on, when solving a problem, make sure to convert all give numbers to the standard units above!
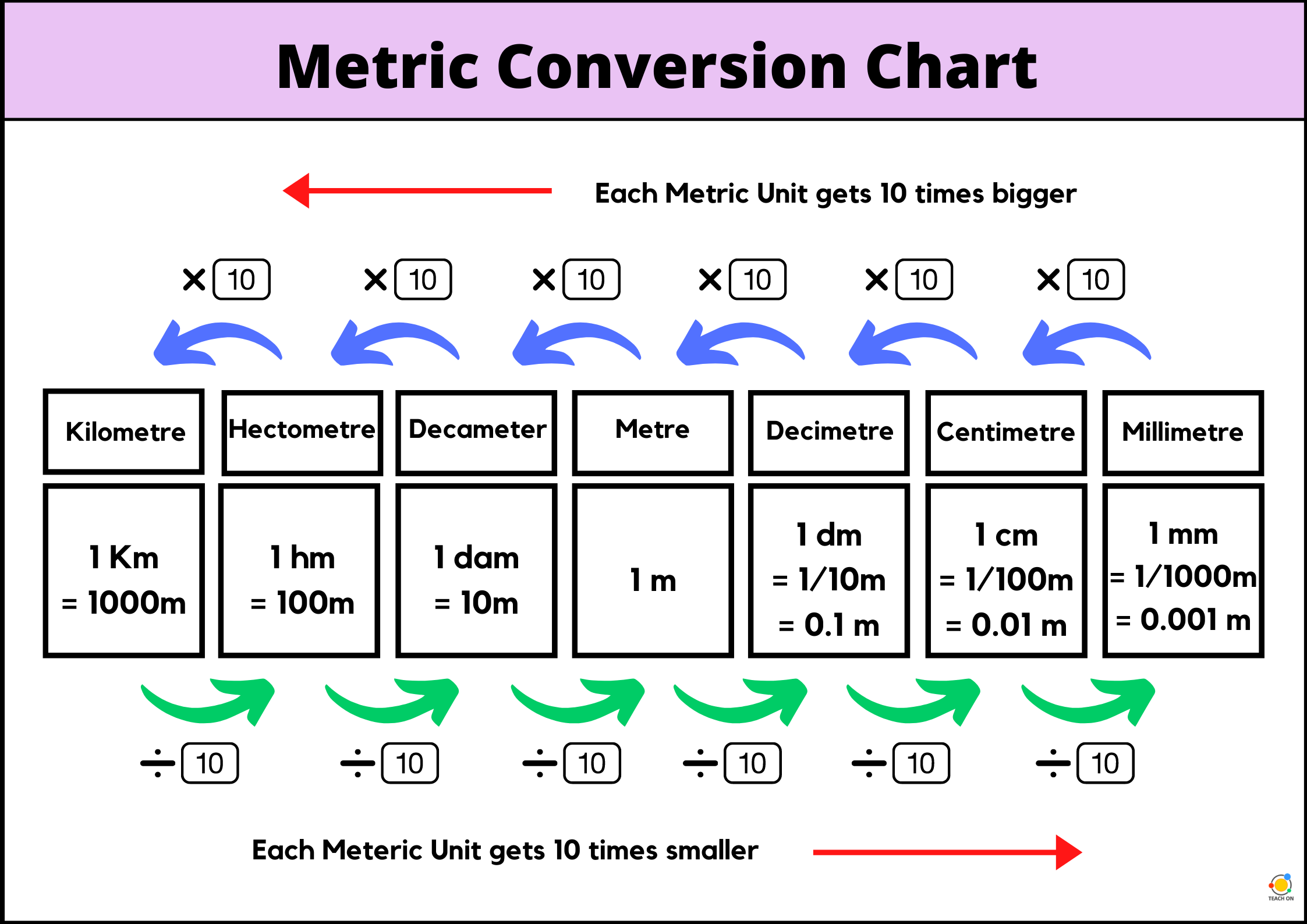
Unit Conversions
As mentioned earlier, converting units is pretty easy in the metic system.
You just have to memorize what each prefix means. The chart below will help with that.
As you do more Physics problems, unit conversions will become super easy!
AND ff you are having trouble converting units, watch this simple video explanation.
PQ Converting Units
Solve ALL problems before checking your answer below.
- Convert 320 grams to kg
- Convert 145 mm to meters
- Convert 100 km/hr the standard unit of velocity used in Physics
- Convert 50 cm/min to m/s
- Convert 365 days to seconds
- Given that 1 inch = 2.54 cm convert 4674 inches to meters
- The volume of a steel cube is 300 cm3. Convert this to m3
- The density of a iron sphere is 7.9 g/cm3. Convert this to kg/m3
Show answers 1 to 4
1. .32 kg
2. .144 m
3. 27.8 m/s (In Physics we use ‘ m/s ‘ as a unit of speed and velocity)
4. .0083 m/s
Show answers 5 to 8
5. 3.15 x 107 s or 31500000 s
6. 118.7 m
7. 3 x 10-4 m3 or .0003 m3
8. 7900 kg/m3
Lesson 1.2 Preview
In the next lesson we will begin to cover kinematics by exploring the 3 kinematic variables: displacement, velocity, and acceleration. We will use standard units. In lesson 1.4 we will begin to utilize our knowledge of vectors to real world problems.
