Unit 1 Breakdown
You are on Lesson 2 of 5
- Unit 1.1 | Understanding vectors and the Standard Units used in Physics
- Unit 1.2 | The Kinematic (motion) variables: Displacement, Velocity, and Acceleration [Current Lesson]
- Unit 1.3 | Graphing motion
- Unit 1.4 | Using Kinematic Equations in 1 Dimension
- Unit 1.5 | Projectile Motion: Using Kinematic Equations in 2 Dimensions
In this lesson you will learn:
- Kinematics and kinematic variables
- Understanding distance vs displacement
- Understanding speed vs velocity
- Understanding acceleration
Kinematics
Kinematics is the study of motion. For anything that moves, we will be able to use kinematics to analyze the motion with graphs and equations.
In this lessons we will cover the kinematic variables: displacement, velocity, and acceleration. In the next lesson we will cover the kinematic equations in order to start solving problems.
Kinematic Variables
As mentioned there are 3 very important kinematic variables: displacement, velocity, and acceleration.
This might seem easy to understand, but it can get be pretty confusing.
Pay attention to bold words and their meanings.
For example speed and velocity do not mean the same thing.
Distance and displacement sound similar. But they are not the same.
Displacement
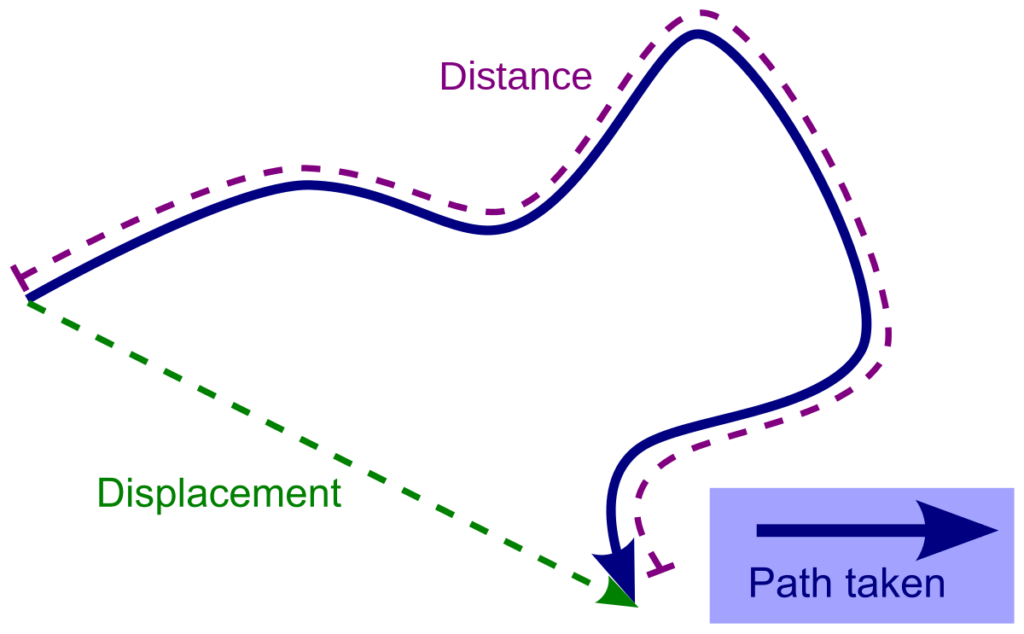
Position ([katex]x[/katex])
Position (a scalar quantity) is where we are. It’s like your home on a map.
We can specify a position using coordinates. Place your finger anywhere on the solid line above – that will be your position.
Displacement ([katex]\Delta x[/katex])
In kinematics, displacement (a vector quantity) is how far we are from our starting point.
Imagine taking a ruler and drawing the dotted green line on the diagram above. This line represents your displacement.
Lets say you run 1 lap around a 100 m. What’s your displacement?
Since you started and ended at the same spot, your displacement is 0.
Your distance traveled is 100 meters.
Displacement is written as [katex]\Delta x[/katex]. The “[katex]\Delta[/katex]” symbol is the greek letter for delta which means “change in.”
Mathematically:
[katex]\Delta x = x_f – x_i[/katex]
This equation simply states that displacement is the change in the final position from the initial position.
Distance (s)
Lastly, Distance (a scalar quantity) is the total amount traveled.
Take your finger and trace out the entire purple path. The total amount your finger traveled is what we call distance.
Let’s say you took a 200-km trip to LA and came back. What’s the distance traveled and displacement?
Show Answer
Your displacement ([katex]\Delta x[/katex]) is zero, because you’re back where you started.
Your distance, however, is 400 kilometers (200 km to go and 200 km back).
PQ – Displacement
Find the distance and displacement of each scenario below.
Note that displacement is written as [katex]\Delta x[/katex] and distance is written as ‘[katex]s[/katex]’.
Question 1: Tyler runs 2 km south, then turns around and runs 3 km north.
Show Answer
[katex]s[/katex] = 5000 m
[katex]\Delta x[/katex] = 1000 m North
*Remember to put answer in standards units. The standard unit for distance/displacement is meter
Question 2: Ash runs exactly 2 laps around a 400 meter track.
Show Answer
[katex]s[/katex] = 800
[katex]\Delta x[/katex] = 0
Question 3: Derrick walks 4 meters south, and then turns east and crawls 6 meters.
Show Answer
[katex]s[/katex] = 10 m
[katex]\Delta x[/katex] = 7.2 m SE
Question 4: You spin around 5 times without moving any direction.
Show Answer
[katex]s[/katex] = 0 m
[katex]\Delta x[/katex] = 0 m
Question 5: Kylie swam 3 complete laps in a 50 meter pool. (1 lap is one length of the pool)
Show Answer
[katex]s[/katex] = 150 m
[katex]\Delta x[/katex] = 50 m
Question 6: John flies directly east for 20,000 m then turns to the north and flies for another 10 km.
Show Answer
[katex]s[/katex] = 30,000 m
[katex]\Delta x[/katex] = 22,400 m
*Remember to put answer in standards units. The standard unit for distance/displacement is meters.
Velocity
In Kinematics, velocity (a vector quantity) is your how fast you move in a specific direction: riding a bike 5 m/s north.
Then what is speed?
Velocity is how fast displacement changes.
Speed is how fast distance changes.
They are similar, but not same. Mathematically:
average velocity ([katex]v[/katex]) = displacement/time = [katex] \frac{\Delta x}{t} [/katex]
average speed = distance/time = [katex] \frac{d}{t} [/katex]
Suppose you run 100 meters around a track in 100 seconds. Find (a) your average speed and (b) your average velocity.
a) your average speed is 100m/100s = 1m/sec.
b) your average velocity is 0m/100s = 0m/sec. (Remember, displacement is 0, when running a full lap!)
Practice Question – Velocity
Answer the questions below and check your answers given in the bold. Remember to use standard units.
- A high school bus travels 240 km in 6.0 h. What is its average speed for the trip? (11.11 m/s)
- A caterpillar travels, north across the length of a 2.00 m porch in 6.5 minutes. What is the average velocity of the caterpillar? (5.1 x 10-3 m/s)
- A hiker is at the bottom of a canyon facing the canyon wall closest to her. She is 280.5 m from the wall and the sound of her voice travels at 340.0 m/s at that location. How long after she shouts will she hear her echo. (1.65 s)
- A motorist traveling on a straight stretch of open highway sets his cruise control at 90.0 km/h. How far will he travel in 15 minutes? (23,000 m)
- A runner completes a 200 meter circular track in 100 seconds. What is his average speed? His average velocity? (2 m/s, 0 m/s)
- A man walks 7 km East in 2 hours and then 2.5 km West in 1 hour. Find his average speed and average velocity. (speed = .89 m/s, v = 4.2 m/s east)
- Sally drove 120 km south at 60 km/h and then 150 km east at 50 km/h. Determine Sally’s speed and magnitude of velocity. (speed = 15 m/s, |v| = 10.67 m/s)
- Challenge: A cross-country rally car driver sets out on a 100.0 km race. At the halfway marker (50.0 km), her pit crew radios that she has averaged only 80.0 km/h. How fast must she drive over the remaining distance in order to average 100.0 km/h for the entire race? (36.94 m/s)
Acceleration
Acceleration (another vector quantity) is how quick velocity changes.
This can be a bit tricky, but let’s break it down.
Let’s say you are traveling 1 m/s north. The next second you are traveling 2 m/s north. And the next second, 3 m/s north.
We can say that our velocity is increasing by 1 m/s north every second. Also written as a 1 m/s2 acceleration North.
Mathematically we can write acceleration as:
[katex] a = \frac{\delta v}{\Delta t} [/katex]
Acceleration Example
Now let’s say you’re riding a bike.
If you start pedaling faster, you are accelerating.
If you hit the brakes, you’re also accelerating – just in the opposite direction (this is also called de-acceleration)!
In simple terms: Acceleration means to speed up. De-acceleration means to slow down.
Units for acceleration
In kinematics, acceleration is denoted by the variable ‘[katex]a[/katex]’ and has the units meters per second squared ([katex]m/s^2[/katex]).
Take the acceleration [katex]9.81 \, m/s^2[/katex]. This tells us, for every second the speed increases by 9.81 m/s.
We call this type of acceleration “gravity.” (more on this later)
A unique instance of acceleration
Acceleration is a vector. It gets it’s direction from the direction of velocity.
The “magnitude of velocity, however, does not always have to change. Instead the direction of velocity can be changing.
Imagine driving a car at constant speed but moving around a circular track.
Your can would be accelerating! Even though the magnitude of velocity remains the same, the direction of velocity changes as the car moves around in a circle. And since velocity changes, the car is infact accelerating.
We call this a “centripetal acceleration.” We will cover this later in Unit 3.1.
In summary, acceleration is defined as the rate of change of velocity over time. Acceleration can be caused by a change in speed or direction.
Practice Questions – Acceleration
Answer the questions below and check your answers given in the bold. Remember to use standard units.
Question 1: If the speedometer of your car reads a constant speed of 40 km/hr, can you say 100% for sure that the car has a constant velocity? Explain your answer.
Show Answer
No we can’t. If the car is changing directions (i.e. moving around a corner) then the direction of velocity changes. A change in velocity means the car is accelerating.
Question 2: A roller coaster start from a speed of 4 m/s and rapidly picks up speed as it rolls down a slope. 3 seconds later, at the bottom of the slope, its speed is 22 m/s. What is its average acceleration?
Show Answer
acceleration = ∆v/t = (22-4)/3 = 6 m/s2
Question 3: A ball is dropped from the top of a building. After 2 seconds, it’s velocity is measured to be 19.6 m/s. Calculate the acceleration for the dropped ball.
Show Answer
[katex]9.81 \, m/s^2[/katex]. This also is the acceleration due to gravity.
Question 4: Falling objects drop with an average acceleration of 9.8 m/s2 (acceleration due to gravity). If an object falls from a tall building, how long will it take before it reaches a speed of 49 m/s?
Show Answer
5 seconds.
Acceleration tells us how fast velocity changes. In this case velocity changes by 9.8 m/s every second. So in 2 seconds it travels 19.6 m/s. In 3 seconds it travels 29.4… and if you continue this pattern, in 5 seconds the object reaches a velocity of 49 m/s.
Question 5: Explain the difference between uniform acceleration and non-uniform acceleration.
Show Answer
Uniform acceleration is the same thing as “constant acceleration.” It is where acceleration stays at one value. For example gravity is a uniform acceleration of 9.81 m/s2. It is this value everywhere on the surface of earth. ALL problems in this course will involve uniform (constant acceleration)
Non-uniform acceleration means the acceleration is changing. For example: acceleration changes from [katex]10 \, m/s^2[/katex] to [katex]5 \, m/s^2[/katex].
We do NOT typically deal with this in a beginner physics course. Generally this will be in an upper level physics class that uses calculus.
LRN Displacement, Velocity, and Acceleration
If you are still a bit confused, below is a video where I re-explain the concepts covered in this lesson.
PQ – All Kinematic Variables
This link will take you to an interactive quiz made by the Physics Classroom. Take the quiz to test your knowledge of displacement, velocity, and acceleration.
Using Variables in Kinematics
You now properly understand the 3 main kinematic variables.
But where are we going to use them?
The remaining lessons in this unit will focus on utilizing the kinematic variables in motion graphs (lesson 1.3) and the big 4 kinematic equations (lesson 1.4) to solve real life problems. This is about to become a lot more interesting!
PQ1 – Kinematics
Before moving on to the next lesson it important to test your understanding. Attempt the questions below.
Question 1: While Mark is traveling north along a straight road, he notices a marker that reads 260 km. Mark keeps traveling north until he reaches the 150 km marker. He then retraces his path back to the 175 km marker. What is marks total displacement from the 260 km marker?
Show Answer
85 km north. NOTE: you must get the direction to get the full point.
Displacement is how far you are from your starting point. Mathematically we can write that displacement = ∆x = xf -xi = 260 – 175.
Question 2: A satellite moving at 1000 km/hr makes 10 complete orbits around the earth in 24 hours. The earth’s radius is 6400 km. What is the satellite’s total displacement around the earth?
Show Answer
0 km. Displacement is how far you are from the starting point. Mathematically it is final position – initial position. The satellite starts and ends at the same position after 10 complete orbits, thus has a displacement of 0.
Question 3: You are running a marathon. From the starting line you travel 1 km north, 7 km east, 20 km south, 7 km east, and then 7 km back up north. What was your total distance traveled? Bonus questions: What was your total displacement from the starting line?
Show Answer
42 km. Distance traveled is the sum of all the smaller distances traveled: 1+7+20+7+7 = 42.
PQ2 – Kinematics
Question 4: Light from the sun reaches the Earth in 8.3 minutes. The velocity of light is 3 x 108 m/s. How far from the Earth is the sun?
Show Answer
1.5 x 1011 meters. NOTE: You must remember to use standard units when solving physics problems. Time should be converted to seconds. And final answer should be meters/second.
You can simply use distance = speed x time to find the solve.
Question 5: On certain planet the acceleration due to gravity is 50 m/s2. Let’s assume you drop a ball from really high up. After 5 seconds how fast is the ball moving?
Show Answer
250 m/s.
50 m/s2 really means that for every second that passes the ball increases its speed by 50 m/s, hence 50 meters per second per every second.
So after 50 m/s in the first second. 100 m/s in 2 seconds. 150 m/s in 3 seconds. And 250 m/s in 5 seconds.
Question 6: You drive your car north for 2 hours at 50 km/hr. Then for the next 3 hours drive at north 100 km/hr. What was you average velocity for your 5 hour drive?
Show Answer
80 km/hr north. OR 22.22 m/s north.
Average velocity is a vector. Thus the formula for average velocity is displacement ÷ time.
Lesson 1.2 Recap
Let’s take a moment to recap what we’ve learned.
First, we explored how kinematics, the study of motion, would be used.
We thoroughly understood the 3 main kinematic variables of displacement, velocity, and acceleration. Then you got plenty of practice to gain an even deeper understanding.
If you are still having trouble understanding, redo the lesson, and remember, practice questions are the key to mastering these concepts. So, keep on exploring and practicing!
Lesson 1.3 Preview
In the next lesson we will the three kinematic variables to create graphs. This may sound boring, but graphs are an incredible tool to help us visualize motion.


